Question

Задание 5.

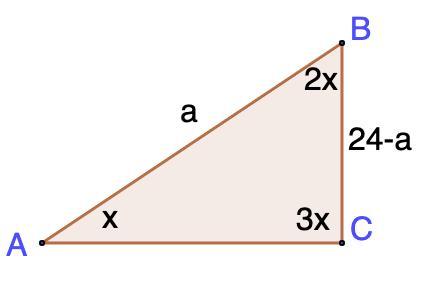
В треугольнике ABC ∠ A : ∠ B : ∠ C = 1 : 2 : 3.

А. Найдите градусные меры углов данного треугольника и определите вид треугольника ABC (13 баллов).

Б. Вычислите длину стороны AB, если AB + BC = 24 (12 баллов).

Answer 1

Ответ:

А. ∠A = 30°;   ∠B = 60°;   ∠C = 90°

∠ABC - прямоугольный.

Б. Длина стороны АВ равна 16 ед.

Объяснение:

В треугольнике ABC ∠ A : ∠ B : ∠ C = 1 : 2 : 3.

А. Найдите градусные меры углов данного треугольника и определите вид треугольника ABC (13 баллов).

Б. Вычислите длину стороны AB, если AB + BC = 24 (12 баллов).

Дано: ΔАВС;

∠A : ∠B : ∠C = 1 : 2 : 3

AB + BC = 24

Найти: А. ∠А; ∠В; ∠С; Б. АВ.

Решение:

А. Пусть ∠А = х, тогда ∠В = 2х, ∠С = 3х

• Сумма углов треугольника равна 180°.

⇒   ∠A + ∠B + ∠C = 180°

х + 2х + 3х= 180°

6х = 180°   |:6

x = 30°

⇒ ∠A = 30°;   ∠B = 60°;   ∠C = 90°

∠ABC - прямоугольный.

Б. АВ + ВС = 24

Пусть АВ = а, тогда ВС = 24 - а

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ АВ = 2 ВС

а = 2 (24 - а)

а = 48 - 2а

3а = 48    |:3

a = 16

⇒ AB = 16

Длина стороны АВ равна 16 ед.