Question

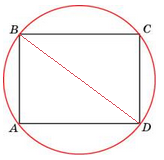
Найдите периметр прямоугольника, если вокруг него описана окружность радиуса 5, а его площадь равна 48.

Answer 1

1) Если прямоугольник вписан в окружность, то его диагональ - диаметр этой окр-сти, тогда ВD= 2*R=2*5=10.

2)Пусть АВ =а, ВС =b, тогда по теореме Пифагора а^2+b^2=BD^2

                                                                             а^2+b^2=100 

C другой стороны: a*b= 48. Решим систему ур-ий:

   { а^2+b^2=100 

     a*b= 48          I *2 и сложим уравнения

 

 { а^2+b^2=100 

    2* a*b= 48 *2

______________

  а^2+b^2+ 2* a*b =196

  (a+b)^2= 14^2  

   a+b= 14

 P = 2*(a+b) =2*14=28

Ответ : 28.