Предмет: Математика,
автор: anntymmm
!!!!SOOOS!!!!
30минут
Приложения:
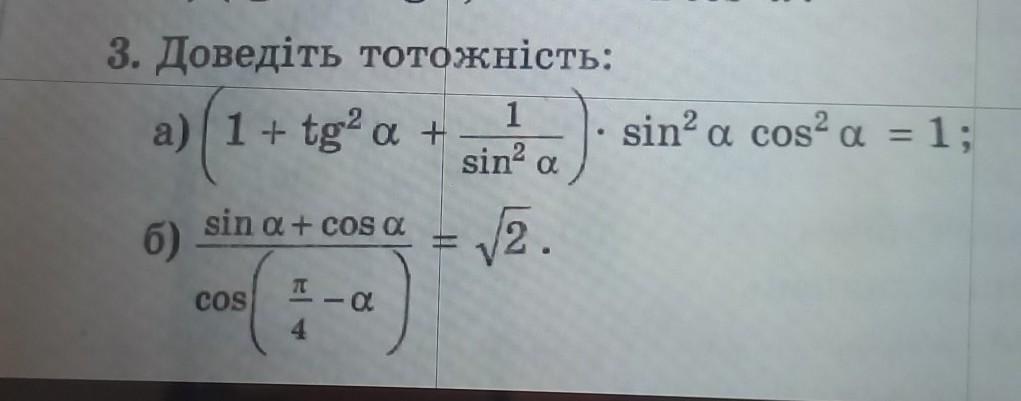
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: isabaevadaana461
Предмет: Қазақ тiлi,
автор: stahokulia1987
Предмет: Українська мова,
автор: riloskosofia
Предмет: Математика,
автор: lizzieh