В правильной треугольной пирамиде боковая грань наклонена к плоскости под углом альфа. Расстояние от основания высоты пирамиды до ее апофемы равно l. Найдите: а) апофему пирамиды б) боковую поверхность пирамиды Будьте добры, с чертежом, это очень важно, так как больше всего я нуждаюсь в том, чтобы понять задачу.
Ответы
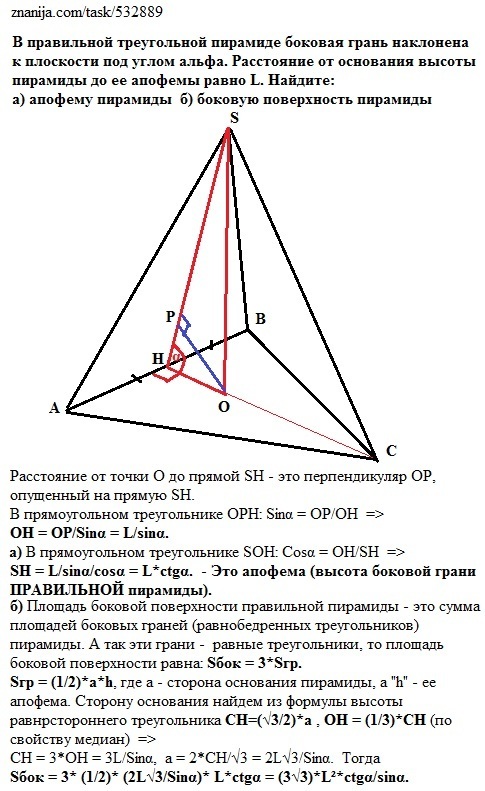
Нам дана правильная пирамида. Значит ее основание - правильный треугольник, а боковые грани - равные равнобедренные треугольники. Кроме торго, вершина пирамиды проецируется в центр основания - точку О пересечения медиан (высот и биссектрис правильного треугольника) основания.
Высота боковой грани правильной (и только правильной!) пирамиды называется ее АПОФЕМОЙ.
Расстояние от точки О до прямой SH (апофема) - это перпендикуляр ОР, опущенный из точки О на прямую SH.
В прямоугольном треугольнике ОРН: Sinα = OP/OH =>
ОН = ОР/Sinα = L/sinα.
а) В прямоугольном треугольнике SОН: Cosα = OH/SH =>
SH = L/sinα/сosα = L*ctgα. - Это апофема (высота боковой грани ПРАВИЛЬНОЙ пирамиды).
б) Площадь боковой поверхности правильной пирамиды - это сумма площадей боковых граней (равнобедренных треугольников) пирамиды. А так как эти грани - равные треугольники, то площадь боковой поверхности равна: Sбок = 3*Sгр.
Sгр = (1/2)*а*h, где а - сторона основания пирамиды, а "h" - ее апофема. Сторону основания найдем из формулы высоты равнрстороннего треугольника СН=(√3/2)*а . Отрезок ОН = (1/3)*СН (по свойству медиан) =>
CH = 3*OH = 3L/Sinα, a = 2*CH/√3 = 2L√3/Sinα. Тогда
Sбок = 3* (1/2)* (2L√3/Sinα)* L*ctgα = (3√3)*L²*ctgα/sinα.