Question

4. Дана функция у=х2 - 10x + 21. [3 6] а) Найдите вершины параболы с помощью формул.
b) Определите точки пересечения с осями координат с) Начертите график функции.

Answer 1

Ответ:

Объяснение:

у=х^2 - 10x + 21.

а) Найдите вершины параболы с помощью формул.

х^2 - 10x + 21 =0.

a=1;  b=-10;  c=21.

x=-b/2a = -(-10)/2*1 = 10/2 = 5;

Подставим в уравнение

y=5^2-10*5+21 = 25-50+21 =  -4.

Вершина параболы в точке C(5;-4).

b) Определите точки пересечения с осями координат

При x=0 (пересечение с осью Оу)

y=0^2-10*0+21 = 21 => A(0;21).

При y=0  x^2-10x+21 = 0;

По т. Виета

x1+x2=10;

x1*x2=21;

x1=3;

x2=7.

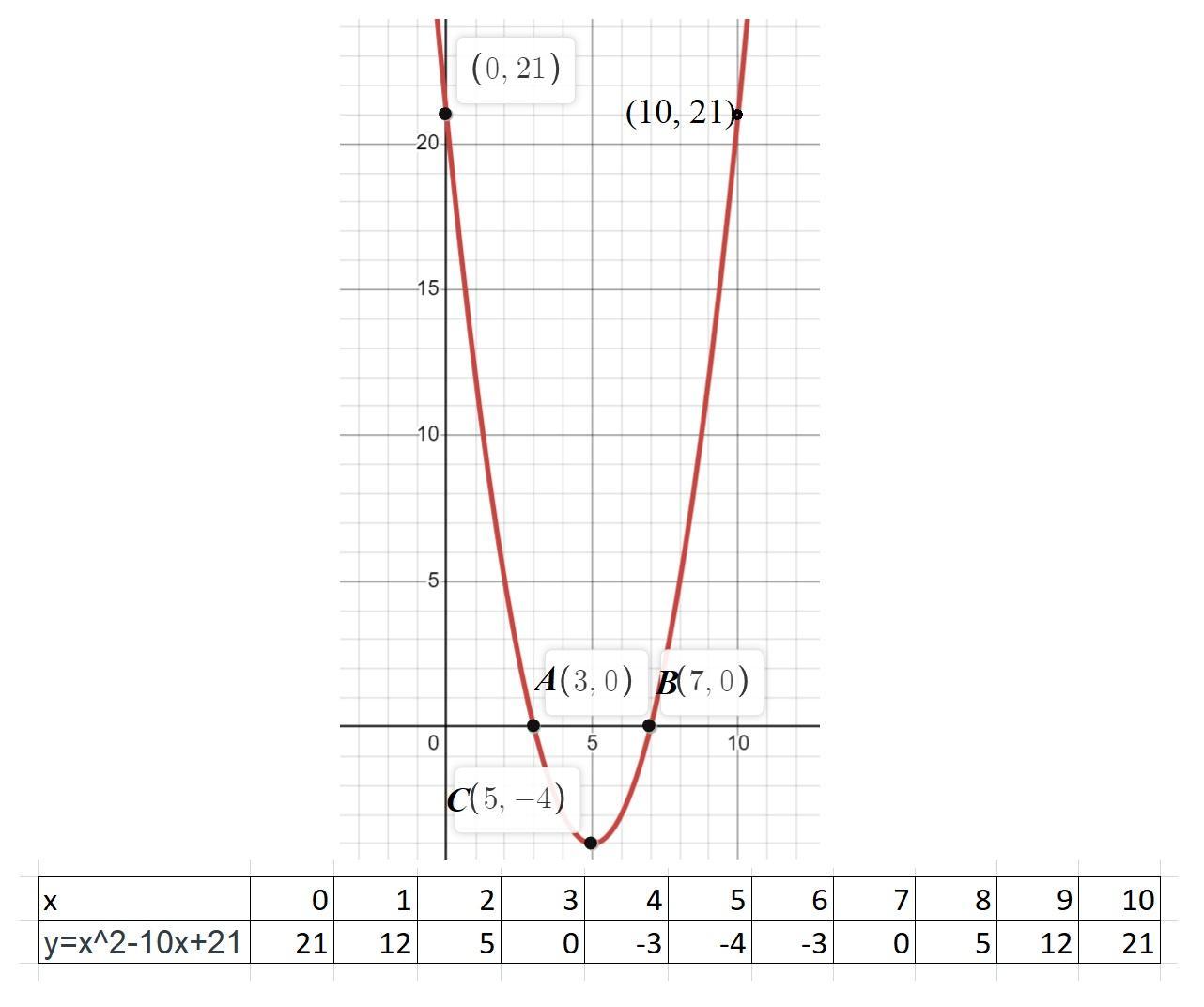
с) Начертите график функции. (См. скриншот)