Question

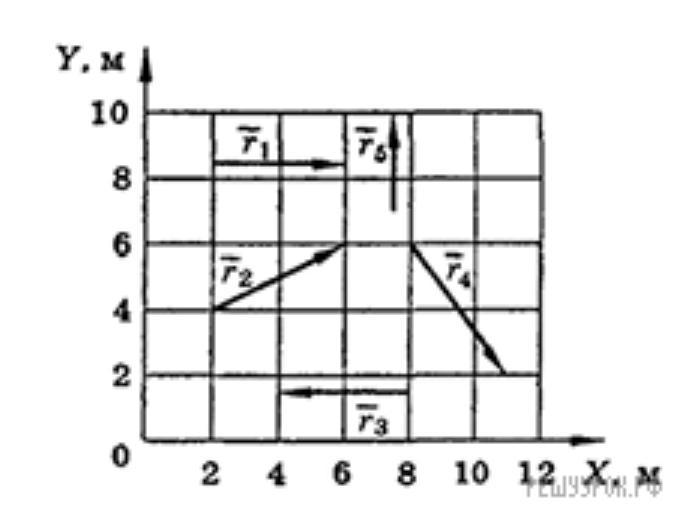
проекцию вектора на каждую ось, найти модуль каждого вектора

Answer 1

Ответ:

r = $\sqrt{r_{x}^2 +r_{y}^2 }$

r1x = (6 - 2) м = 4 м

r1y = 0

r1 = $\sqrt{r_{1x}^2 +r_{1y}^2 }$=4 м

r2x = (6 - 2) м = 4 м

r2y = (6 - 4) м = 2 м

r2 = $\sqrt{r_{2x}^2 +r_{2y}^2 }$ = $\sqrt{20}$ = $2\sqrt{5}$

r3x = (4 - 8) м = -4 м

r3y = 0

r3 = $\sqrt{r_{3x}^2 +r_{3y}^2 }$ = 4 м

r4x = (11 - 8) м = 3 м

r4y = (2 - 6) м = -4 м

r4 = $\sqrt{r_{4x}^2 +r_{4y}^2 }$ = 5 м

r5x = 0

r5y = (10 - 7) м = 3 м

r5 = $\sqrt{r_{5x}^2 +r_{5y}^2 }$ = 3 м

Объяснение:

Проекция вектора на координатную ось равна разности координат конца и его начала.