Question

Докажите, что если сторона, прилежащий к ней угол и сумма 2 других сторон одного треугольника соответственно равны стороне, прилежпщему к нему углу и сумме 2 других сторон другого треугольника, докажите, что такие треугольники равны. Пожалуйста, решение не из интернета, я не могу его понять, заранее спасибо

Answer 1

Для того, чтобы лучше разобраться с доказательством, можно ввести дополнительные обозначения.

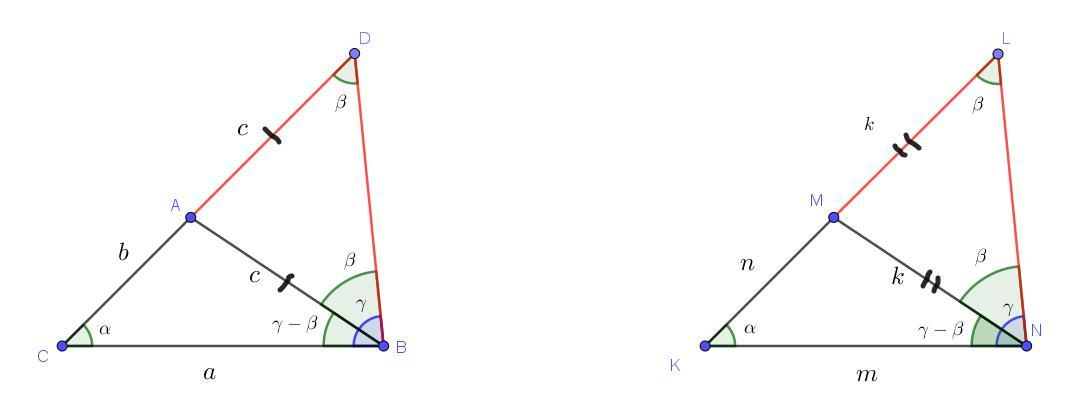
Пусть нам по условию даны 2 треугольника: АВС и KMN со сторонами соответственно a,b,c и m,n,k

Также нам известно, что у них по одной равной стороне (пусть a=m),

есть равный угол прилежащий к равным сторонам (пусть ∠C=∠K=α) и суммы оставшихся двух сторон равны (то есть b+c=n+k).

Так как у нас есть информация про стороны и угол, то можно воспользоваться первым признаком равенства треугольников:

По двум сторонам и углу между ними.

Чтобы им воспользоваться, отложим у первого треугольника отрезок AD равный стороне c, а у второго треугольника - ML равный стороне k.

Теперь у нас появились новые треугольники: CDB и KLN, которые уже равны как раз по первому признаку (∠C=∠K; CB=KN CD=b+c, KL=n+k, а по условию b+c=n+k ⇒ CD=KL)

Так как треугольники равны, значит равны и оставшиеся элементы, то есть ∠D=∠L=β и ∠DBC=∠LNK=γ

Мы откладывали отрезок AD равный отрезку AB ⇒ ΔADB - равнобедренный ⇒ ∠ABD=∠ADB=β.

Аналогично в ΔMLN: ∠MLN=∠LNM=β.

В ΔАВС: ∠ABC=∠DBC-∠DBA=γ-β

В ΔKMN: ∠MNK=∠LNK-∠LNM=γ-β

Таким образом, для треугольников АВС и MNK:

a=m; ∠ACB=∠MKN=α; ∠ABC=∠MNK=γ-β ⇒ треугольники равны по стороне и двум прилежащим углам (второй признак равенства треугольников) - ч.т.д.