Question

зовнішній кут трикутника=125; знати суму двох внутрішніх кутів трикутника не суміжних з ним

*Задача не з підручника*

Answer 1

Ответ:

Внешний угол треугольника равен сумме двух несмежных с ним внутренних углов

<1+<2=125*
Внешний угол треугольника и смежный ему внутренний в сумме равны 180*
<3=180-125=55*

Объяснение:

Answer 2

Відповідь: 125°

Згідно теореми  зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів трикутника, не суміжних з ним ,то якщо зовнішній кут 125°,то сума внутрішніх,не суміжніх з ним кутів дорівнює 125°

Пояснення:

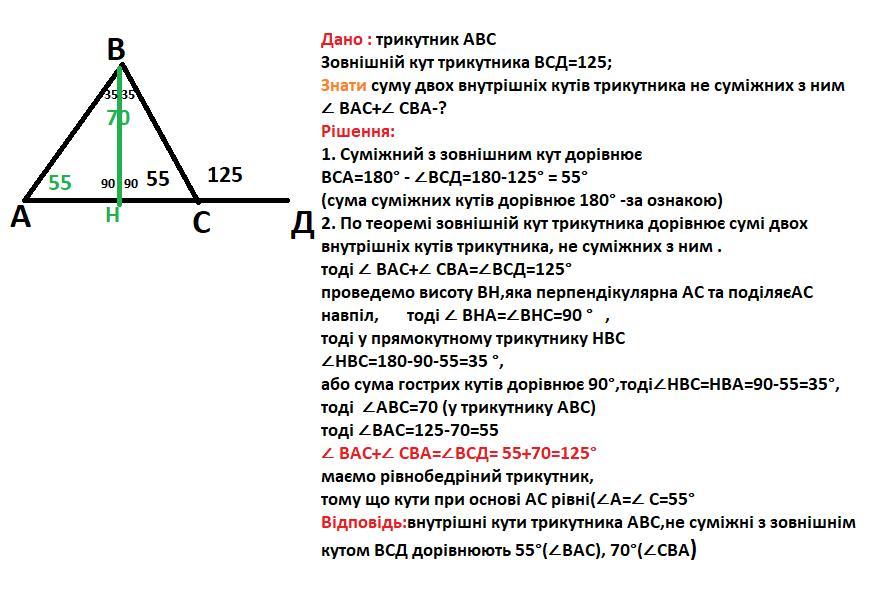
Дано : трикутник АВС

Зовнішній кут трикутника ВСД=125;

Знати суму двох внутрішніх кутів трикутника не суміжних з ним

∠ ВАС+∠ СВА-?

Рішення:

1. Суміжний з зовнішним кут дорівнює                                                                 ВСА=180° - ∠ВСД=180-125° = 55°                                                                                                       (сума суміжних кутів дорівнює 180° -за ознакою)

2. Згідно з теоремою  зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів трикутника, не суміжних з ним .

тоді ∠ ВАС+∠ СВА=∠ВСД=125°

проведемо висоту ВН,яка перпендікулярна АС та поділяєАС навпіл,       тоді ∠ ВНА=∠ВНС=90 °   ,                                                                                                                тоді у прямокутному трикутнику НВС                                                                  ∠НВС=180-90-55=35 °,                                                                                       або сума гострих кутів дорівнює 90°,тоді∠НВС=НВА=90-55=35°,

тоді  ∠АВС=70 (у трикутнику АВС)

тоді ∠ВАС=125-70=55

∠ ВАС+∠ СВА=∠ВСД= 55+70=125°

маємо рівнобедріний трикутник,                                                                                 тому що кути при основі АС рівні(∠А=∠ С=55°                         Відповідь:внутрішні кути трикутника АВС,не суміжні з зовнішнім кутом ВСД дорівнюють 55°(∠ВАС), 70°(∠СВА)