Question

Точка дотику кола, виписано в рівнобічну трапецію. ділить її бічну сторону на відрізки 2 см і 8 см. Знайдіть площу трапеції.​

Answer 1

Відповідь:

S(трап.)=80 (см²)

Пояснення:

Точка дотику кола, виписано в рівнобічну трапецію

ділить її бічну сторону на відрізки   2 см і 8 см.

Знайдіть площу трапеції.​

Розв'язання:

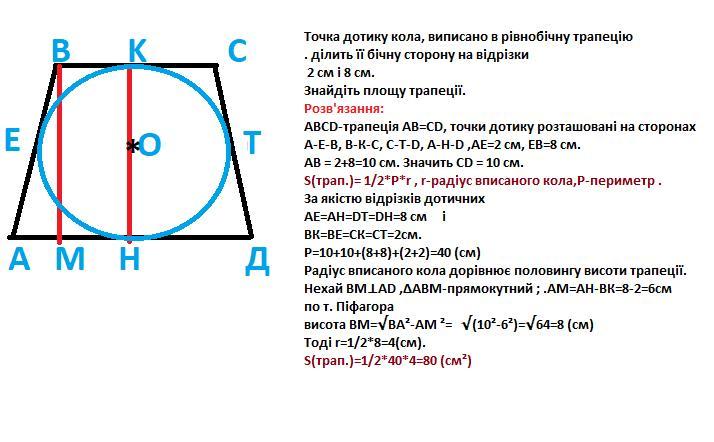
АВСD-трапеція АВ=СD, точки дотику розташовані на сторонах

А-Е-В, В-К-С, С-Т-D, А-Н-D ,АЕ=2 см, ЕВ=8 см.

АВ = 2+8=10 см. Значить СD = 10 см.

S(трап.)= 1/2*Р*r , r-радіус вписаного кола,Р-периметр .

За якістю відрізків дотичних                                                                                                                     АЕ=АН=DT=DH=8 см     і

ВК=ВЕ=СК=СТ=2см.    

Р=10+10+(8+8)+(2+2)=40 (см)

Радіус вписаного кола дорівнює половингу висоти трапеції.

Нехай ВМ⊥АD ,ΔАВМ-прямокутний ; .АМ=АН-ВК=8-2=6см

Згідно т. Піфагора                                                                                                                                                                      висота ВМ=√ВА²-АМ ²=   √(10²-6²)=√64=8 (см)

Тоді r=1/2*8=4(см).

S(трап.)=1/2*40*4=80 (см²)