Предмет: Физика,
автор: beyixo4819
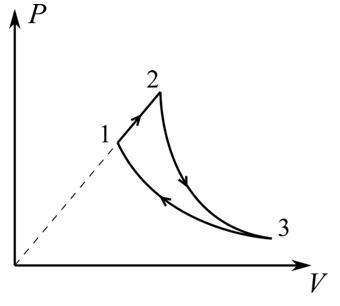
Два моля одноатомного газа совершает цикл. 1-2-3. состоящий из участка, на котором давление прямо пропорционально объему адиабатического расширения и изотермического сжатия. В изотермическом процессе над газом совершена работа 570 Дж. КПД цикла η = 15%. Найти разность максимальной и минимальной температур в адиабатическом процессе. Ответ выразить в Кельвинах с округлением до целого числа.
Приложения:
Ответы
Автор ответа:
1
В процессе 1-2 газ совершает работу, равную площади трапеции. Но ее же можно найти как разность площадей двух прямоугольных треугольников с катетами и
и
и
Этот процесс является нагревателем (теплота газу передается) и поэтому
Отметим что разность температур в этой формуле и есть искомая разность температур. Процесс 2-3 не является ни нагревателем, ни холодильником, а вот процесс 3-1 это холодильник. Работа в этом процессе попросту известна Дж (знак минус потому что над газом) и как следствие
Для КПД в итоге имеем формулу
Откуда
Похожие вопросы
Предмет: Математика,
автор: vasulunaholunska
Предмет: Физика,
автор: nastyayushchenko2306
Предмет: Українська література,
автор: vslnkavasa
Предмет: Геометрия,
автор: Kkamai
Предмет: Математика,
автор: Novincho