Предмет: Алгебра,
автор: ivanustimenko162
помогите, не могу решить
Приложения:
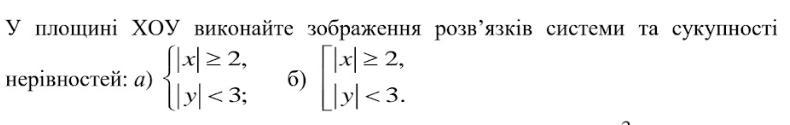
Ответы
Автор ответа:
2
Ответ:
Решением системы является пересечение множеств , то есть их общая часть .
Рисунок 1 (область заштрихована) .
Область |x| ≥ 2 - это множество точек плоскости, расположенных левее прямой х = -2 и правее прямой х = 2 . Сами прямые х = -2 и х = 2 входят в эту область .
Область, заданная неравенством |y| < 3 - это множество точек плоскости, расположенных между прямыми у = -3 и н = 3 . Сами прямые в область не входят .
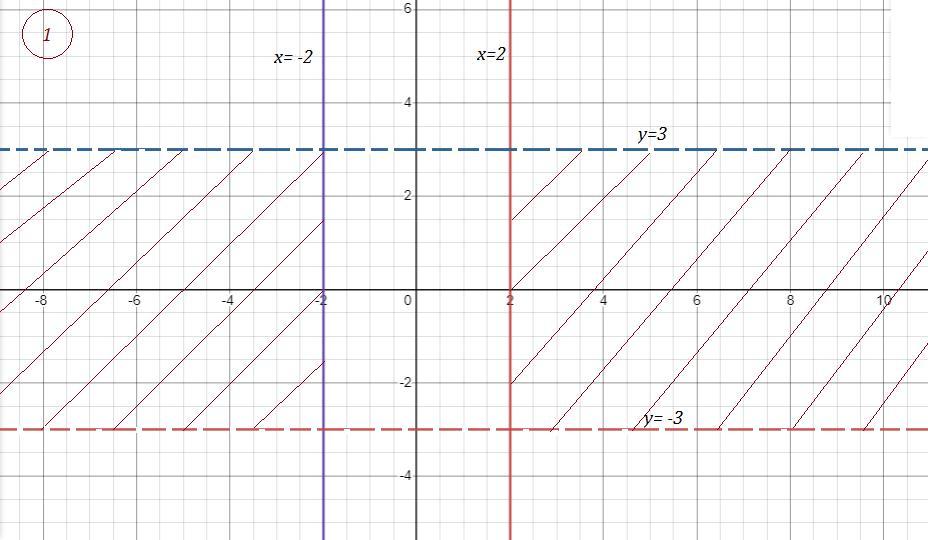
Решением совокупности является объединение множеств , то есть то, что принадлежит и первому и второму множествам .
Рисунок 2 (область заштрихована) .
Приложения:

Похожие вопросы
Предмет: Математика,
автор: Danil2069
Предмет: Математика,
автор: hyygffffhgdsahswwqws
Предмет: Українська мова,
автор: gret98666
Предмет: Геометрия,
автор: Kkamai