Предмет: Геометрия,
автор: salammolekym
знайдіть площу бічної поверхні та площу повної поверхні правильної трикутника призми Сторона основи якої дорівнює 8 см, а висота призми - 12 см.(писати на листочку з малюнком)
Ответы
Автор ответа:
1
Ответ:
Sбок. = 288(см)², Sполн. = 288 + 32√3(см)²
Объяснение:
Найдите площадь боковой поверхности и площадь полной поверхности правильной треугольника призмы, сторона основания которой равна 8 см, а высота призмы - 12 см.
------------------------------------------------------
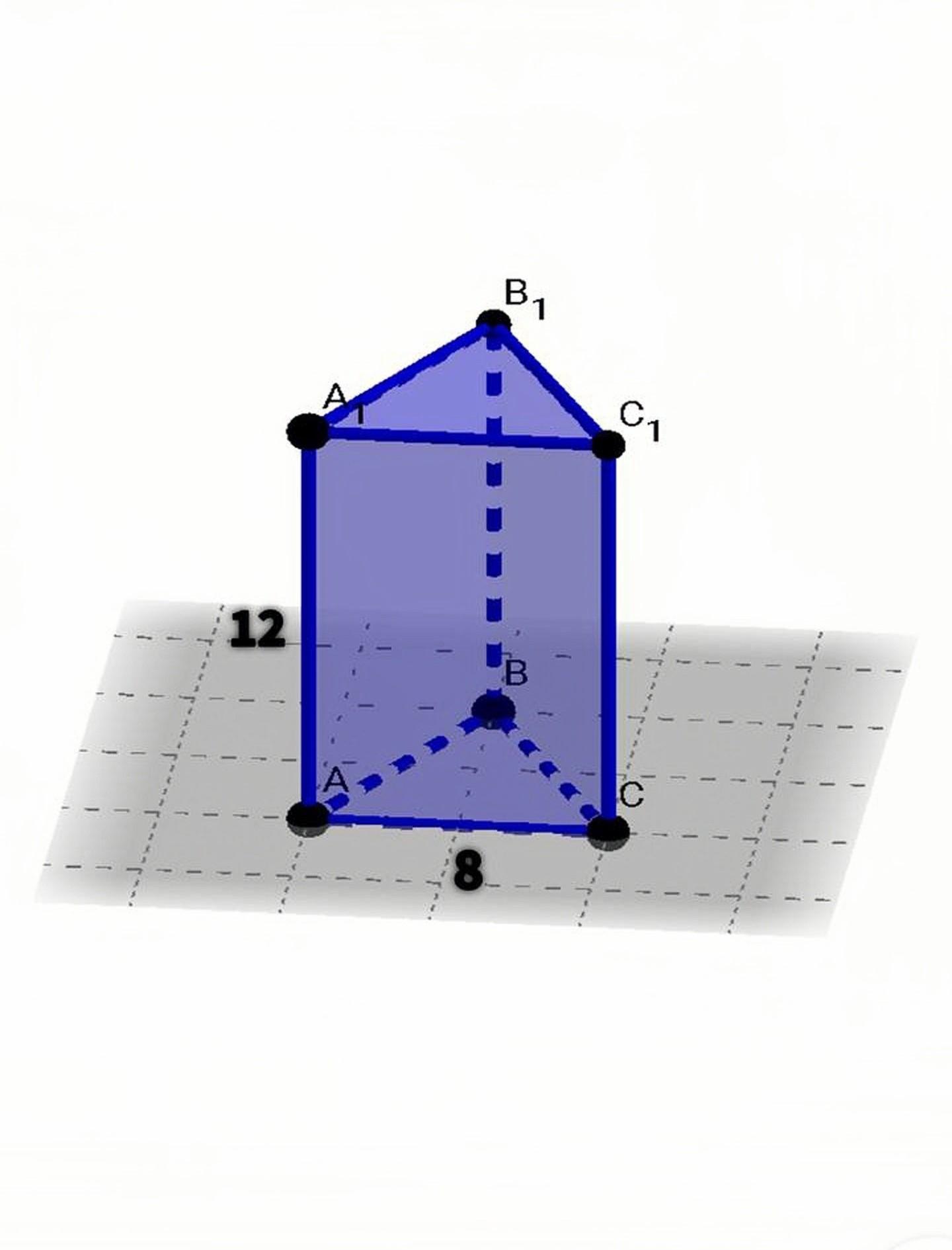
Дано: ABCA₁B₁C₁ – правильная треугольная призма, АА₁ = 12см, АС = 8см.
Найти: Sбок. и Sполн.
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение
- Площадь боковой поверхности призмы вычисляется по формуле: Sбок. = Росн. * h, где Росн. - периметр основания, h - высота призмы. Т.к. призма правильная, то ее высота совпадает с ее боковым ребром.
- Основание правильной треугольной призмы - равносторонний треугольник, периметр которого вычисляется по формуле: Р = 3а, где а - сторона треугольника.
⠀⠀⠀Росн. = 3 * 8 = 24(см)
⠀⠀⠀Sбок. = 24 * 12 = 288(см)²
- Площадь полной поверхности призмы вычисляется по формуле: Sполн. = Sбок. + 2Sосн, где Sбок. – площадь боковой поверхности, Sосн. – площадь основания. Т.к. в основании лежит равносторонний треугольник, то ее площадь вычисляется по формуле:
, где а - сторона треугольника.
⠀⠀⠀
- Найдем площадь полной поверхности:
⠀⠀⠀Sполн. = 288 + 2 * 16√3 = 288 + 32√3(см)²
Ответ: Sбок. = 288(см)², Sполн. = 288 + 32√3(см)²
Приложения:
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Литература,
автор: kzdml15dor
Предмет: Физика,
автор: shatalova2005
Предмет: Українська мова,
автор: nirorgir
Предмет: Окружающий мир,
автор: Аноним