Предмет: Алгебра,
автор: iMich
Срочно будласочка даю 100 балів
5. Знайдіть найбільший цілий розв'язок нерівності ((x - 1) ^ 2)/(x + 2) <= 0
Приложения:
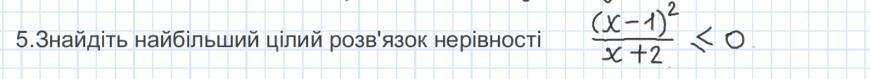
Ответы
Автор ответа:
2
Ответ: 1 — найбільше ціле рішення нерівності
Объяснение:
Очевидно, что числитель всегда будет неотрицательным числом, поскольку он является полным квадратом, значит данная дробь будет меньше нуля, когда знаменатель будет меньше нуля т.е
x + 2 < 0
x < - 2 ⇒ наибольшее целое решение равно (-3)
Но незабудем, о частном случае, когда дробь равна нулю
В случае x = 1 неравенство выполняется и т.к 1 > - 3, то 1 — наибольшее целое решение неравенства
Можно решить методом интервалов, выйдет также
Похожие вопросы
Предмет: Алгебра,
автор: polina1786
Предмет: История,
автор: tyreasweq
Предмет: Химия,
автор: natali1332
Предмет: Математика,
автор: yegorberezhnoy