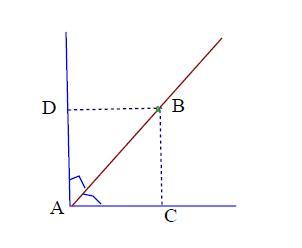
Точка внутри прямого угла одинаково удалена от сторон угла. Её расстояние от вершины угла 5 корня из 2. Н-ти расстояние от точки до сторон угла.
Пожалуйста с рисунком умоляю.
Ответы
Ответ:
Объяснение:
Дано:
∠А = 90°
DВ = СВ
АВ =5√2
____________
DВ = СВ= ?
Решение.
1) Т.к. точка равно удалена от сторон угла, то, значит, она лежит на биссектрисе.
Биссектриса угла делит этот угол пополам. Т.к. ∠А =90°, то
∠DАB = ∠ВАС = 90°/2 = 45°
2) В ΔАВС:
∠ВСА = 90° по построению.
Т.к. ∠ВАС = 45°, то и ∠АВС= 45° (сумма всех угловΔ-ка = 180°). Следовательно, ΔАВС - равнобедренный. АС = ВС.
По т.Пифагора АВ² = АС² + ВС² = 2ВС²
(5√2)² =2ВС²
25*2 = 2ВС²
25 = ВС²
ВС = √25 = 5.
Т.к. точка равноудалена от сторон ∠А, то
BC = DB =5
Или: ∠ВСА = 90° и ∠BCD= 90° по построению.
Следовательно, ADBC - прямоугольник, у которого противоположные стороны равны, т.е.
DB = АС и DA = ВС, но по условию, DB = CB, значит, ADBC - квадрат:
DB = АС = DA = ВС.
Если известна диагональ квадрата d (d = АВ =5√2), то длина его стороны a может быть вычислена с помощью следующей формулы:
a = d / √2
а = DB = АС = DA = ВС = 5√2/√2 =5.