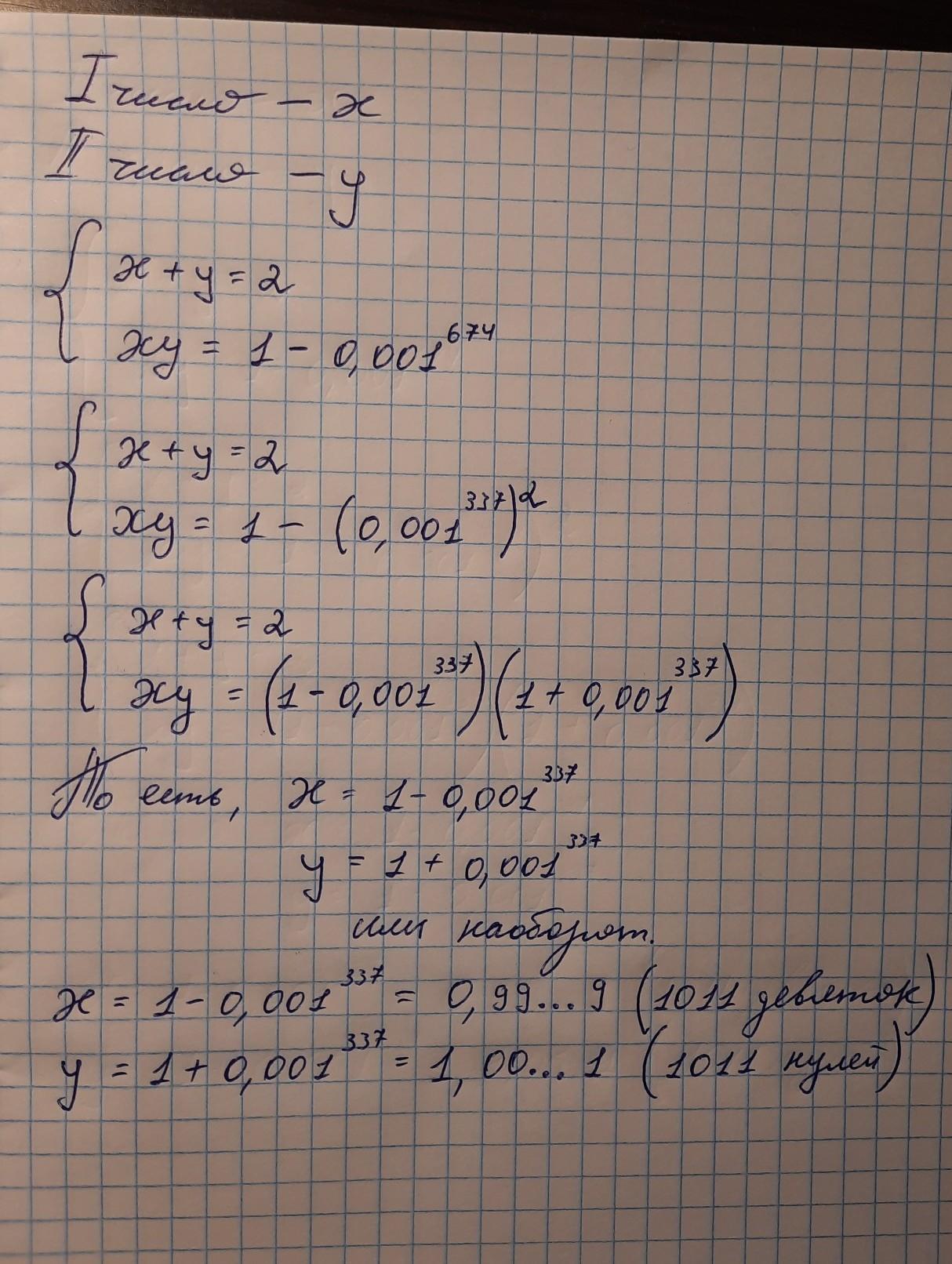это вообще возможно решить? вообще олимпиада закончилась уже как 10 месяцев назад, но до сих пор интересно, как это решить (первая задача), текстовый вариант: найдите 2 рациональных числа, сумма которых равна двум, а их произведение равно 0,99...9(2022 двойки)

Ответы
Пошаговое объяснение:
Пусть 1 число-х, тогда 2 число-у. Логично, что мы будем составлять систему. Первое уравнение системы будет х+у=2( по условию), со вторым же интереснее. Если от 1 вычесть 0,99 будет 0,01, если от 1 вычесть 0,999 будет 0,001. То есть в обоих случаях будет не хватать всего 1 частицы. Так же будет если от 1 вычесть любую другую десятичную дробь у которой после запятой одни девятки, всегда будет не хватать 1 частицы. То есть, для записи 0,99...9(2022 девяток) надо от 1 вычесть число, у которого после запятой сколько же нулей и одна единица сколько у числа 0,99..9(2022 девятки) девяток. Буквально, нужно от 1 - 0,00...1(2022 нуля) чтобы получилось 0,99...9(2022 девяток).Для удобства, используем число 0.001 в степени 674. Почему? Потому что опять же нам нужно 2022 нуля после запятой, а в числе 0,001 у нас уже есть 3 нуля после( 0.001 потому что 2022 нацело делится на 3, чтобы не было дробей в степени). Из этого делаем вывод, что 0,99...9(2022 девятка) можно ещё записать как 1 - 0.001^674. Вот и подошло 2 уравнение системы, которое будет выглядеть как х×у=1-0.001^674. Собираем всё вместе и получим систему как на фото. Далее, вспоминаем формулы сокращенного умножения и свойства степеней. 0.001^674 это тоже самое что и (0.001^337)^2. Теперь просто посмотри решение до конца на фото.