Question

Пожалуйста помогите решить задачу по геометрии, срочно!!!!​

Answer 1

Ответ:

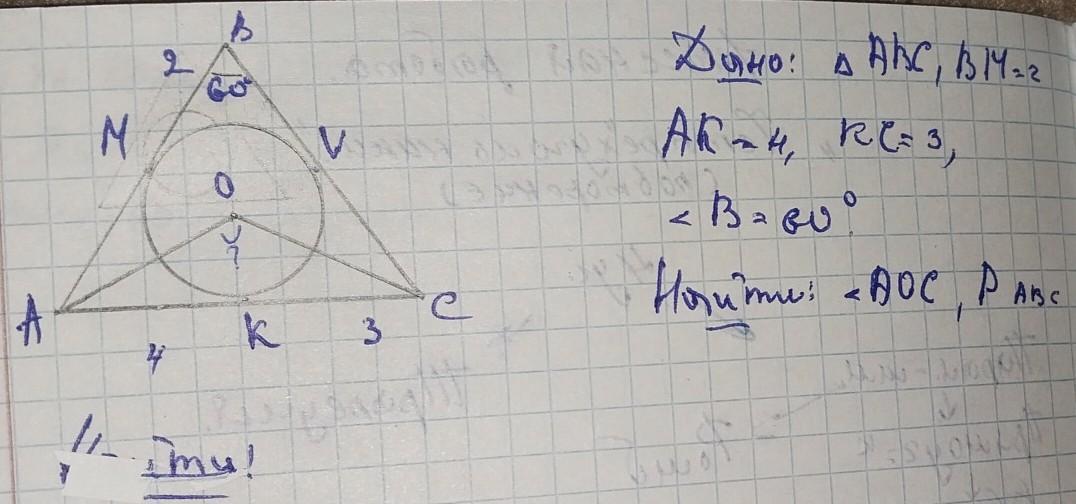
∠АОС=60°; Р(∆АВС)=18ед.

Объяснение:

Две касательные проведенные из одной точки равны между собой.

ВМ=ВV=2ед. (две касательные проведенные из точки В)

КС=СV=3ед. (две касательные проведенные из точки С)

АК=АМ=4ед. (две касательные проведенные из точки А)

Р(∆АВС)=2*ВМ+2*АК+2*КС=

=2*2+2*4+2*3=4+8+6=18 ед.

Сумма углов в треугольнике равна 180°

(∠ВАС+∠ВСА)=180°-∠В=180°-60°=120° Сумма двух углов треугольника ∆АВС.

т.О- точка пересечения биссектрисс.

ОС- биссектриса угла ∠С

АО- биссектриса угла ∠А

Следовательно:

(∠ОАС+∠ОСА)=(∠ВАС+∠ВСА)/2=120°/2=60°

∆АОС

∠АОС=180°-(∠ОАС+∠ОСА)=180°-60°=120°