Предмет: Геометрия,
автор: aizhanaне
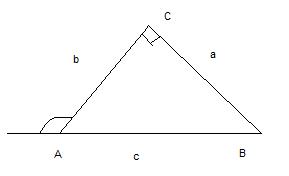
Один из внешних углов прямоугольного треугольника равен 120 градусов. Найдите длину сторон треугольника, если известно, что сумма гипотенузы и меньшего катета равна 20 см.
Ответы
Автор ответа:
0
1. Находим угол А прямоугольного треугольника:
А = 180 - 120 = 60°
Пусть b + с = 20 см, тогда с = 20 - b
2. cosA = , cos60 =
, cos60 = 

2b = 20-b
3b=20
b= =
= 
3. Находим с:
с = 20-b = 20 - =
=  =
= 
4. По теореме Пифагора находим оставшийся неизвестный катет а:
a = √c² - b² = √ ² -
² -  ² = √
² = √ =
=  =
= 
А = 180 - 120 = 60°
Пусть b + с = 20 см, тогда с = 20 - b
2. cosA =
2b = 20-b
3b=20
b=
3. Находим с:
с = 20-b = 20 -
4. По теореме Пифагора находим оставшийся неизвестный катет а:
a = √c² - b² = √
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: medenovanurgul05
Предмет: Українська мова,
автор: JeTix135
Предмет: Литература,
автор: ObitoUchiha1763
Предмет: Математика,
автор: rufan