Question

срочно , задача по геометрии

Answer 1

Ответ:

А₁А₂ = 6 см; A₁B₁ = 5 (см)

Объяснение:

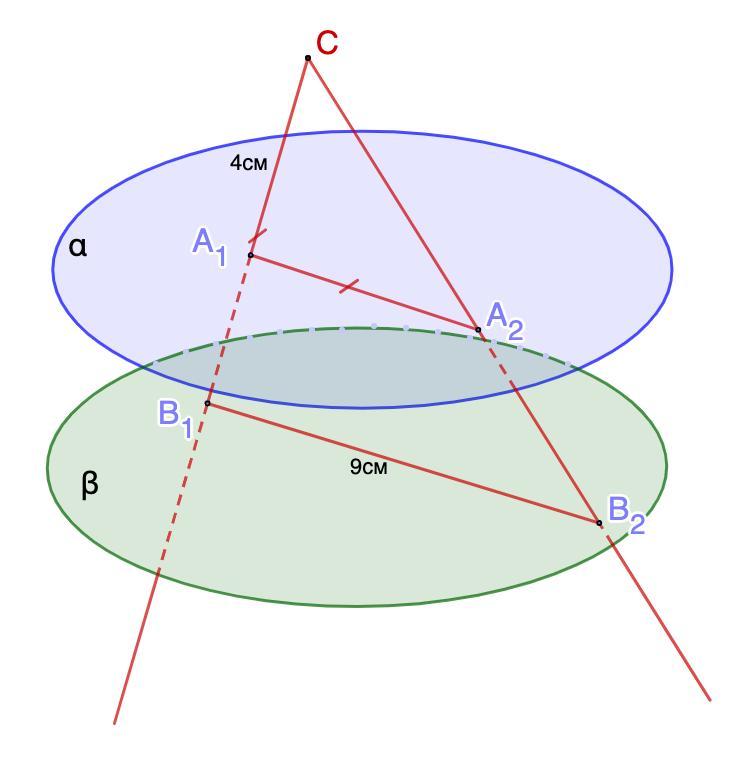
7. Через точку С, не принадлежащую двум параллельным плоскостям α и β, проведены два луча, один из которых пересекает плоскости α и β в точках А₁ и В₁ соответственно, а второй - соответственно в точках А₂ и В₂. Известно, что СА₁ = 4 см, B₁B₂ = 9 см, А₁А₂ = СВ₁. Найдите А₁А₂ и А₁В₁.

Дано: α || β;

C ∉ α; C ∉ β.

СА₁ = 4 см, B₁B₂ = 9 см, А₁А₂ = СВ₁.

Найти: А₁А₂ и А₁В₁.

Решение:

• Через две пересекающиеся прямые можно провести плоскость, причем только одну.

⇒ через СВ₁ и СВ₂ можем провести плоскость.

• Если две параллельные плоскости пересекает третья, то линии пересечения параллельны.

⇒ А₁А₂ || B₁B₂

Рассмотрим ΔА₁СА₂ и В₁СВ₂

∠С - общий;

∠СА₁А₂ = ∠СВ₁В₂ (соответственные при А₁А₂ || B₁B₂ и секущей СВ₁)

⇒ ΔА₁СА₂ ~ В₁СВ₂ (по двум углам)

Пусть А₁А₂ = СВ₁ = а

Запишем отношения сходственных сторон:

$\displaystyle \frac{CA_1}{CB_1}=\frac{A_1A_2}{B_1B_2} \\\\\frac{4}{a}=\frac{a}{9} \;\;\;\Rightarrow \;\;\;a^2=36 \;\;\;\Rightarrow \;\;\;a = 6$

А₁А₂ = 6 см

A₁B₁ = CB₁ - CA₁ = 9 - 4 = 5 (см)

#SPJ1