5x+6y=3, 2) x-2y=-9; 4) x-4y=-42, 9x+8y=62.
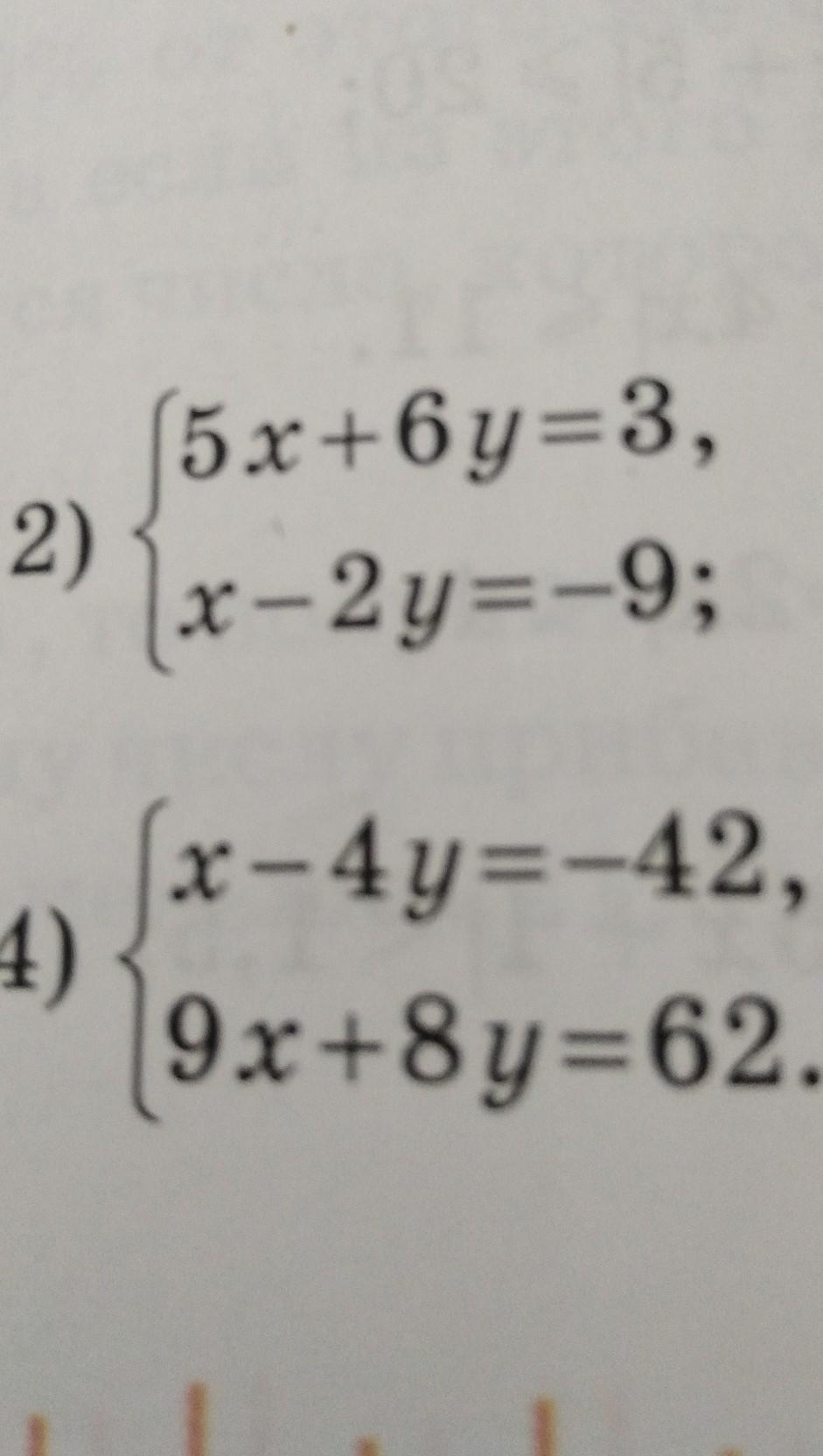
Ответы
Ответ:
Ответ дан ниже
Пошаговое объяснение:
Для вирішення системи рівнянь можемо використовувати метод елімінації:
Почнемо з першої системи рівнянь:
Спочатку помножимо друге рівняння на 3, щоб позбавитися від x:
x - 2y = -9
3x - 6y = -27
Тепер додамо перше рівняння до отриманого другого:
(5x + 6y) + (3x - 6y) = 3 - 27
8x = -24
Розділімо обидва боки на 8:
x = -3
Тепер підставимо x в перше рівняння:
5(-3) + 6y = 3
-15 + 6y = 3
Приберемо -15 з обох боків:
6y = 18
Розділімо обидва боки на 6:
y = 3
Таким чином, перше рівняння має розв'язок x = -3 і y = 3.
Тепер перейдемо до другої системи рівнянь:
Спочатку помножимо перше рівняння на 9, щоб позбавитися від x:
9(x - 4y) = 9(-42)
9x - 36y = -378
Тепер додамо отримане перше рівняння до другого:
(9x + 8y) + (9x - 36y) = 62 - 378
18x - 28y = -316
Далі, додамо перше рівняння до другого:
(9x + 8y) + (9x - 36y) = 62 - 378
18x - 28y = -316
Тепер поділимо обидва боки на 2, щоб спростити:
9x - 14y = -158
Далі, можемо вирішити отримане рівняння:
9x - 14y = -158
9x = 14y - 158
x = (14y - 158) / 9
Це є виразом для x у відношенні до y.
Таким чином, друга система рівнянь не має єдиного розв'язку, і вона визначає x як функцію від y.