Question

Найдите множество значений функции g(x)=(все под корнем) 9 - x^2

Answer 1

Ответ:

1) Всё под корнем можно представить как (3-х)(3+х) и всё это должно быть >= 0

2) Чтобы п. 1 был >= 0, нужно чтобы каждая из скобок была >= 0 ЛИБО обе <= 0 (потому что если перемножить два отрицательных числа, получится положительное). То есть у нас два варианта развития событий:

а) 3-х >= 0

И

3+х >= 0

А значит

-х >= -3

И

х >= -3

А значит

х <= 3

И

х >= -3

б) 3-х <= 0

И

3+х <= 0

А значит

-х <= - 3

И

х <= - 3

А значит

х >= 3

И

х <= - 3

3) Рисуем числовую ось для варианта а)

Отмечаем на ней точки НЕ ВЫКОЛОТЫЕ: - 3, 0, 3. Рисуем/штрихуем всё от - 3 до 3.

Рисуем числовую ось для б)

Отмечаем точки НЕ ВЫКОЛОТЫЕ: - 3, 0, 3.

Рисуем/штрихуем всё что меньше - 3 и всё что больше 3. Визуально видно, что нет таких иксов, которые одновременно < - 3 и вместе с этим > 3. А значит б) нам не подходит.

Область определения функции: [-3;3]

По области определения можно найти область значения. Для этого поставляем найденные иксы в исходное уравнение и пытаемся построить график по этим точкам.

Получается, область значения [0; 3]

Answer 2

Решение .

 Задана функция   $\bf g(x)=\sqrt{9-x^2}$  .

Найти множество значений функции .

Возведём обе части равенства в квадрат , получим  

$\bf g^2=9-x^2\ \ \ \Rightarrow \ \ \ x^2+g^2=9$  

Это уравнение окружности с центром в точке  (0:0) и радиуса R=3 .

Просто функция обозначена не буквой "у" , как привычно, а буквой "g"   ( x²+y²=9 ) .

Для такой окружности функция изменяется от  -3  до  3 :

$\bf -3\leq g(x)\leq 3$  ,

Но квадратный корень  $\bf\sqrt{9-x^2}$  может принимать только неотрицательные значения ,  $\bf\sqrt{9-x^2}\geq 0$  .   Поэтому окончательно получаем

$\left\{\begin{array}{l}\bf -3\leq g(x)\leq 3\ ,\\\bf g(x)\geq 0\end{array}\right\ \ \ \Rightarrow \ \ \ \bf 0\leq g(x)\leq 3$        

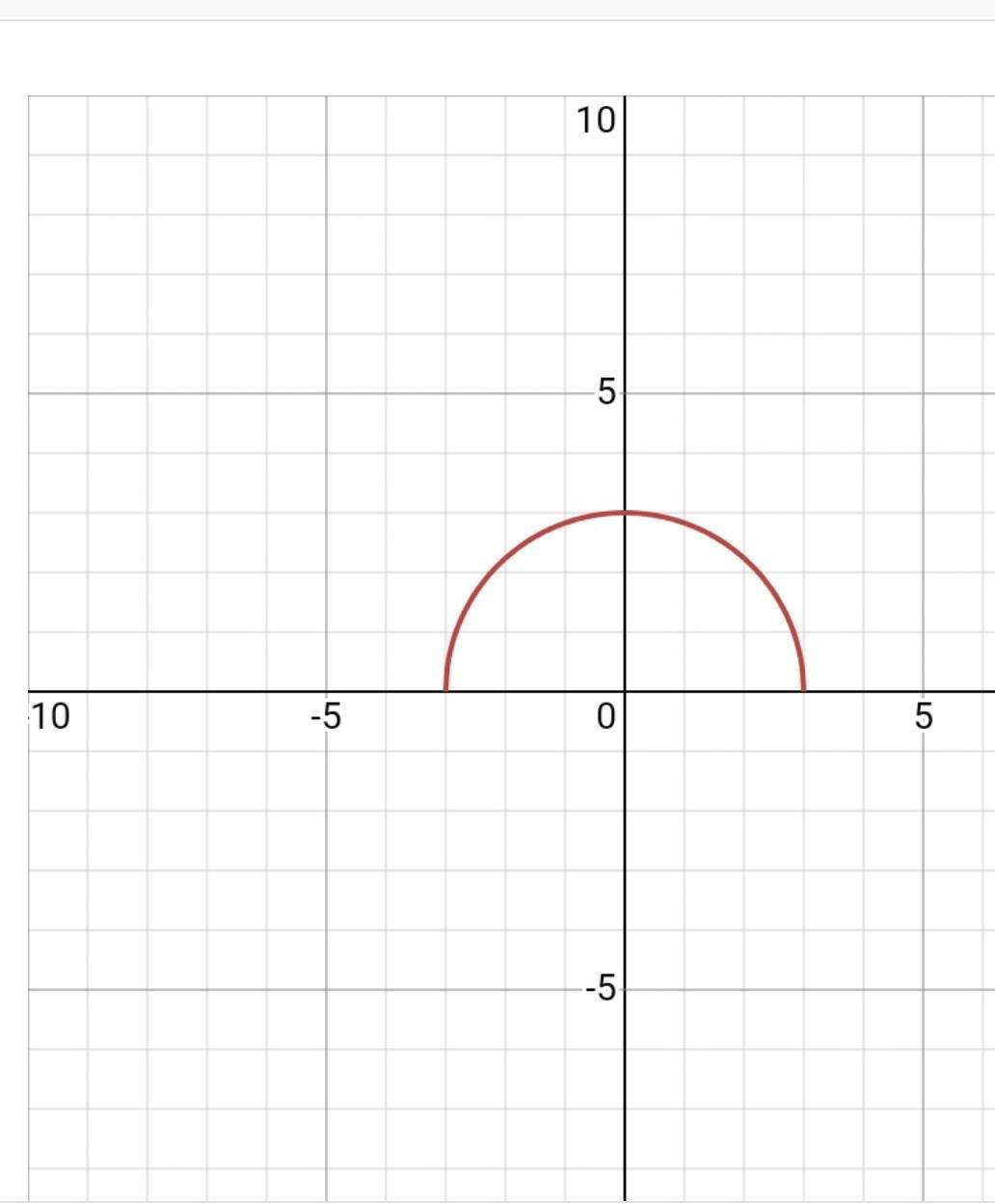
Функция  $\bf g(x)=\sqrt{9-x^2}$   описывает верхнюю полуокружность с центром в точке (0;0) и радиуса R=3 .

Множество значений функции :   $\bf E(y)=[\ 0\ ;\ 3\ ]\ \ ,\ \ y\in [\ 0\, ;\, 3\ ]$   .  

Замечание , Областью определения заданной функции является отрезок :  $\bf D(y)=[-3\, ;\, 3\ ]\ \ ,\ \ x\in [-3\, ;\, 3\ ]$  .