Допоможіть будь ласка вирішити рівняння
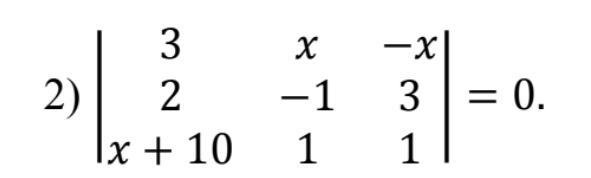
Ответы
Ответ:
Примечание:
Теорема о разложении или теорема Лапласа:
Значение определителя матрицы равно сумме произведений элементов некоторой строки (столбца) на их алгебраические дополнения.
Минором элемента определителя порядка
называется определитель порядка
, полученного из данного вычеркиванием
-й строки и
-го столбца и обозначается в виде
.
Алгебраическим дополнением элемента называют число:
------------------------------------------------------------------------------------------------------
Будем рассматривать элементы матрицы в общем виде в записи:
При сложение элементов какой-либо строки (какого-либо столбца) с соответствующими элементами другой строки (столбца) умноженными на некоторое число определитель матрицы не меняется.
Определитель матрицы не меняется при элементарных преобразованиях матрицы.
- строка с номером n
- столбец с номером n
Пошаговое объяснение:
1)
2)
#SPJ1