Предмет: Алгебра,
автор: akto85568
за 65 баллов, два примера.
Приложения:
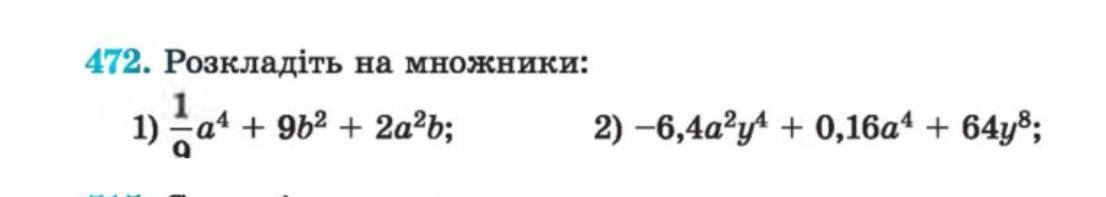
Ответы
Автор ответа:
2
Похожие вопросы
Предмет: Математика,
автор: sokolnikovmaksim01
Предмет: Физика,
автор: ivanmachenik
Предмет: Українська література,
автор: id1619324
Предмет: Математика,
автор: Илья2173
Предмет: Химия,
автор: enatsudr