Предмет: Алгебра,
автор: liliarudenko845
Решить систему уравнений
Приложения:
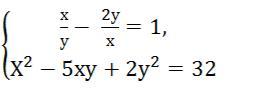
Ответы
Автор ответа:
0
Ответ:
(-2; 2) , (2;-2) , (2√2; √2) и (-2√2; -√2).
Объяснение:
Решить систему уравнений:
Рассмотрим первое уравнение системы
Пусть , тогда
и уравнение принимает вид:
Тогда получим при t= -1 x=-y и при t =2 x=2y.
Тогда решим две системы
(-2; 2) и (2;-2) - решение системы
(2√2; √2) и (-2√2; -√2) - еще два решения системы.
Значит, система имеет 4 решения
(-2; 2) , (2;-2) , (2√2; √2) и (-2√2; -√2)
#SPJ1
Похожие вопросы
Предмет: Алгебра,
автор: p64103533
Предмет: Другие предметы,
автор: DirolWhite
Предмет: История,
автор: kirakora068
Предмет: Физика,
автор: hamzk