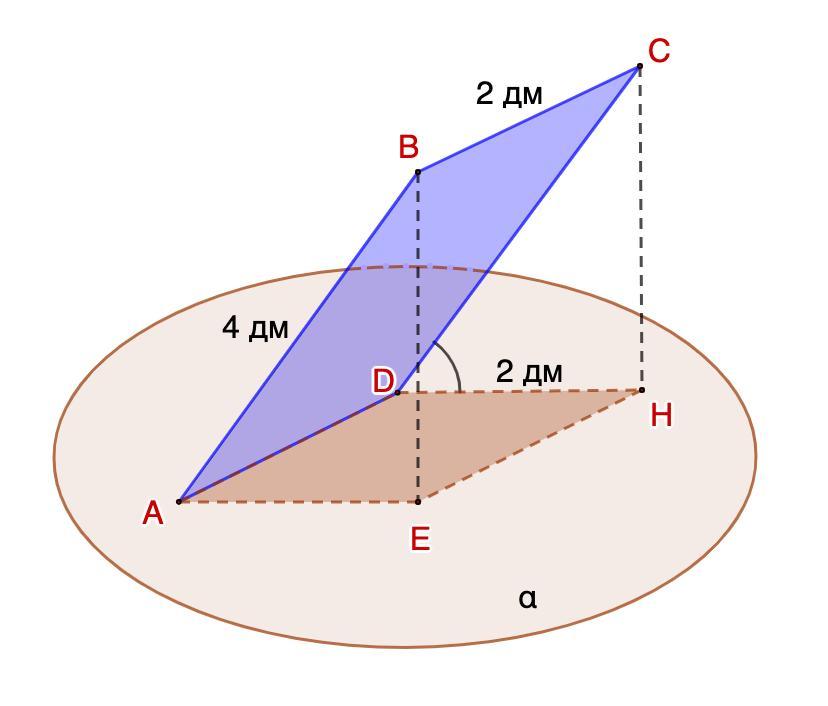
10. Через сторону AD прямоугольника АВСD со сторонами 2 дм и 4 дм проведена плоскость а. Ортогональная проекция прямоугольника на плоскость а - квадрат. Найдите угол наклона прямой CD к плоскости а.

Ответы
Ответ:
Угол наклона прямой CD к плоскости α равен 60°.
Объяснение:
10. Через сторону AD прямоугольника АВСD со сторонами 2 дм и 4 дм проведена плоскость α. Ортогональная проекция прямоугольника на плоскость α - квадрат. Найдите угол наклона прямой CD к плоскости α.
Определимся с длиной сторон прямоугольника.
- Проекцией прямоугольника на плоскость называется фигура, ограниченная проекциями сторон прямоугольника на эту плоскость.
Так как проекция - квадрат, а наклонная всегда больше ее проекции, то AD - меньшая сторона, а СD - большая.
Дано: АВСD - прямоугольник;
АВ = СD = 4 дм, ВС = CD = 2 дм.
АDHE - квадрат, проекция ABCD на плоскость α;
Найти: угол наклона прямой CD к плоскости α.
Решение:
- Угол между прямой и плоскостью - это угол между прямой и ее проекцией на данную плоскость.
⇒ ∠CDH - искомый угол.
АDHE - квадрат.
⇒ AD = DH = EH = AE = 2 дм
Рассмотрим ΔDCH - прямоугольный.
DC = 4 дм, DH = 2 дм.
- Если катет вдвое меньше гипотенузы, то он лежит против угла 30°.
⇒ ∠DCH = 30°
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠CDH = 90° - ∠DCH = 90° - 30° = 60°
Угол наклона прямой CD к плоскости α равен 60°.
#SPJ1