Предмет: Математика,
автор: rkia978
Найдите синус угла B
Как это решить??
Приложения:
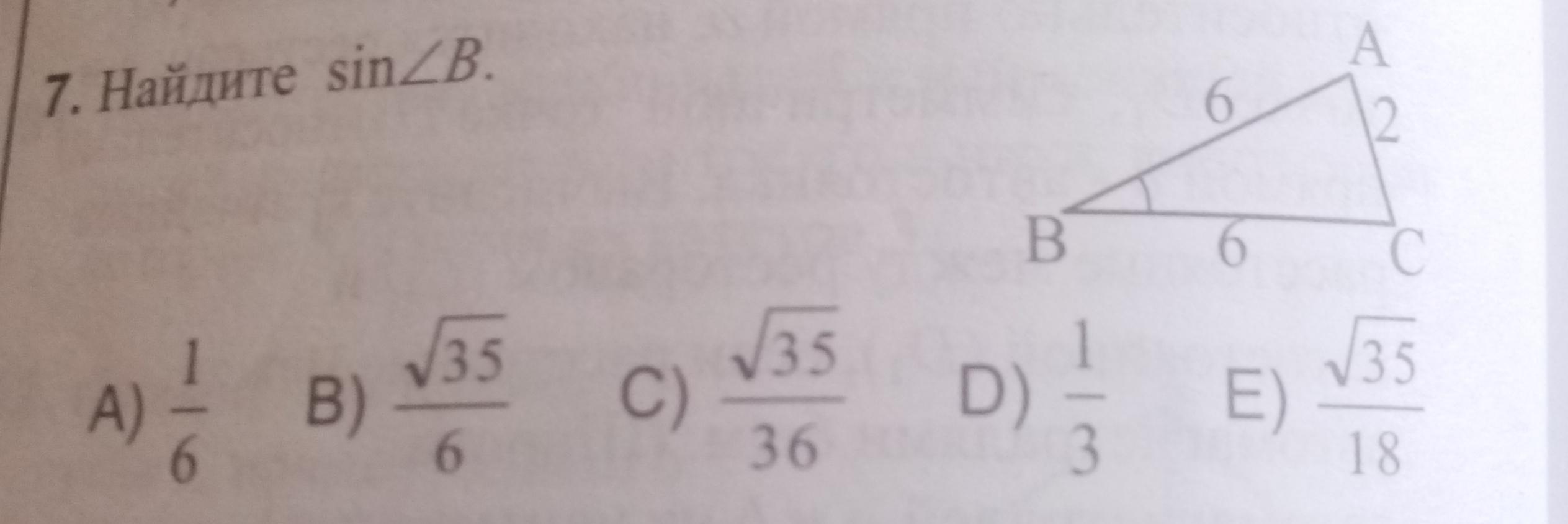
7x8:
E)
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Из закона косинусов
sin∠B
Автор ответа:
1
Ответ: E)
Пошаговое объяснение:
Проведем высоту BD на сторону АС.
Треугольник ADB -прямоугольный.
Похожие вопросы
Предмет: Математика,
автор: aijamaljorobekova
Предмет: Английский язык,
автор: tvybumfb
Предмет: Математика,
автор: pon4aa11
Предмет: Обществознание,
автор: anymm