Предмет: Геометрия,
автор: kyznetsovatamara0362
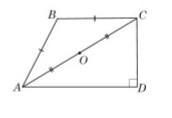
На рисунку зображено прямокутну трапецію ABCD, у якої AB=BC, AC = 40 см, CD = 24 см. До кожного відрізка (1-3) доберiть його дов- жину (А - Д), якщо О- середина діагоналі АС трапеції ABCD.
Приложения:
zmeura1204:
Де рисунок?
щас
Які відрізки?
в и д
Що потрібно знати? У вас має бути таблиця з назвами відрізків.
прямокутного
Ответы
Автор ответа:
2
Ответ:
АD=32см
АВ=25см
ВС=25см
ВD=7см
Объяснение:
∆АСD- прямокутний трикутник
Теорема Піфагора:
АD=√(AC²-CD²)=√(40²-24²)=
=√(1600-576)=√1024=32см
_________
ВС=АВ=НD=x
AH=AD-HD=(32-x)
∆ABH- прямокутний трикутник
За теоремою Піфагора:
BH²+AH²=AB²
24²+(32-x)²=x²
576+(1024-64х+x²)=x²
576+1024-64х+х²-х²=0
-64х=-1600
х=25см
АВ=ВС=25см
_____________
∆BDC- прямокутний трикутник
За теоремою Піфагора:
ВD=√(BC²+CD²)=√(25²+24²)=√49=7сс
Приложения:

Похожие вопросы
Предмет: Алгебра,
автор: lucenkotemka230
Предмет: Геометрия,
автор: melnikira2022
Предмет: Английский язык,
автор: aimanmakeeva
Предмет: Українська мова,
автор: kolosovv07
Предмет: Физика,
автор: diefnkdfjskd