Предмет: Алгебра,
автор: ooooq
срочно! найти область определения функции
Приложения:
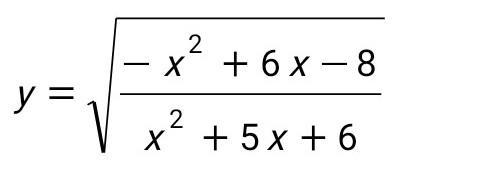
Ответы
Автор ответа:
1
Ответ:
Область определения функции .
Разложим на множители квадратные трёхчлены .
Областью определения функции будет множество значений х , при которых
Знаки функции :
Выбираем промежутки со знаком плюс .
Ответ: .
Приложения:

Похожие вопросы
Предмет: Алгебра,
автор: alinabrovdii016
Предмет: Биология,
автор: ktfk700
Предмет: Музыка,
автор: elvirabojko87
Предмет: Математика,
автор: busiki228
Предмет: Геометрия,
автор: vyacheslavplakhin