Предмет: Математика,
автор: dggfe134
12) В прямоугольном треугольнике ABC (ZC =90°) проведе- на высота СН. Найдите sin ZA, cosZA и tg/A, если CH =12, HB=16-
Ответы
Автор ответа:
0
Ответ:
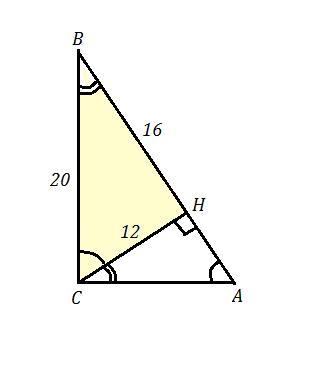
Дан ΔАВС , ∠С = 90° , СН ⊥ АВ , СН = 12 , НВ = 16 .
Найти : sinA , cosA , tgA .
Рассмотрим ΔВСН и ΔАСН . Они оба прямоугольные ,
∠ВНС = 90° , ∠АНС = 90° .
В ΔАВС : ∠ВАС = 90° - ∠АВС = 90° - ∠В .
В ΔАСН : ∠НАС =∠ВАС = 90°-∠АСН , значит 90° - ∠В = 90° - ∠АСН
⇒ ∠АСН = ∠В .
Тогда ∠ВСН = ∠А .
Тогда можно найти тригонометрические функции не ∠А , а ∠ВСН
в ΔВСН , так как Δв этом треугольнике известны два катета,
СН = 12 и НВ = 16 .
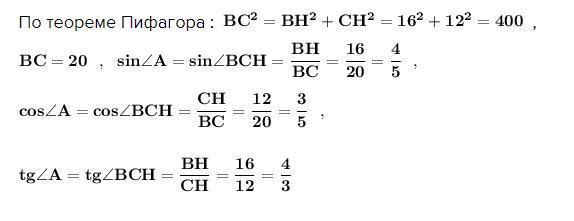
По теореме Пифагора : ,
Приложения:
Похожие вопросы
Предмет: Биология,
автор: zipirina05
Предмет: Английский язык,
автор: kirilylass6
Предмет: Обществознание,
автор: zorik17
Предмет: Математика,
автор: prismotrovi
Предмет: Математика,
автор: kirillpirogov463