Предмет: Алгебра,
автор: tina2722
Доказать, что для любого натурального n выполняется равенство:
Приложения:
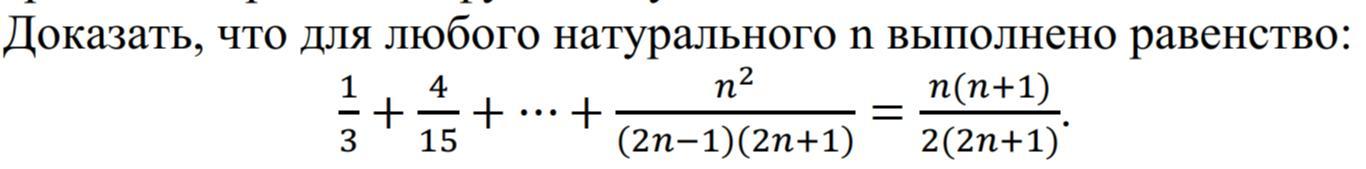
Ответы
Автор ответа:
1
Когда мы сложим много таких слагаемых с различными n, у нас первые слагаемые много раз сложатся, а вот вторые и третьи почти везде уничтожат друг друга. Останется только
и
Поэтому в итоге сумма первых n слагаемых будет равна
Похожие вопросы
Предмет: Геометрия,
автор: dovsdc
Предмет: Биология,
автор: Mashacorso
Предмет: Математика,
автор: valentina1989nik
Предмет: Русский язык,
автор: yarovayelena84
Предмет: Английский язык,
автор: feniksko02