Предмет: Математика,
автор: mshvlad9072
изучить интеграл и в случае сходимости вычислить его
Приложения:
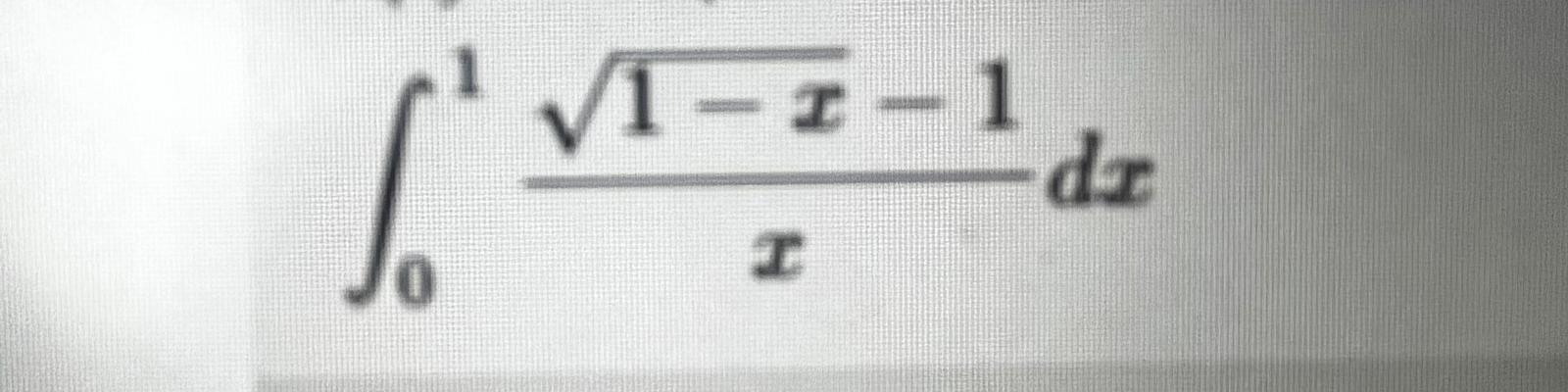
antonovm:
2ln2 - 2
Ответы
Автор ответа:
1
Этот интеграл не является элементарным, поэтому давайте проведем замену переменной. Пусть , тогда
и пределы интегрирования при
имеем
и при
имеем
. Получаем:
Интеграл сходится
Похожие вопросы
Предмет: Английский язык,
автор: xzvgzmq5jf
Предмет: Литература,
автор: lavrenecsofiya
Предмет: Математика,
автор: pipitanev
Предмет: Литература,
автор: shk03032008