Question

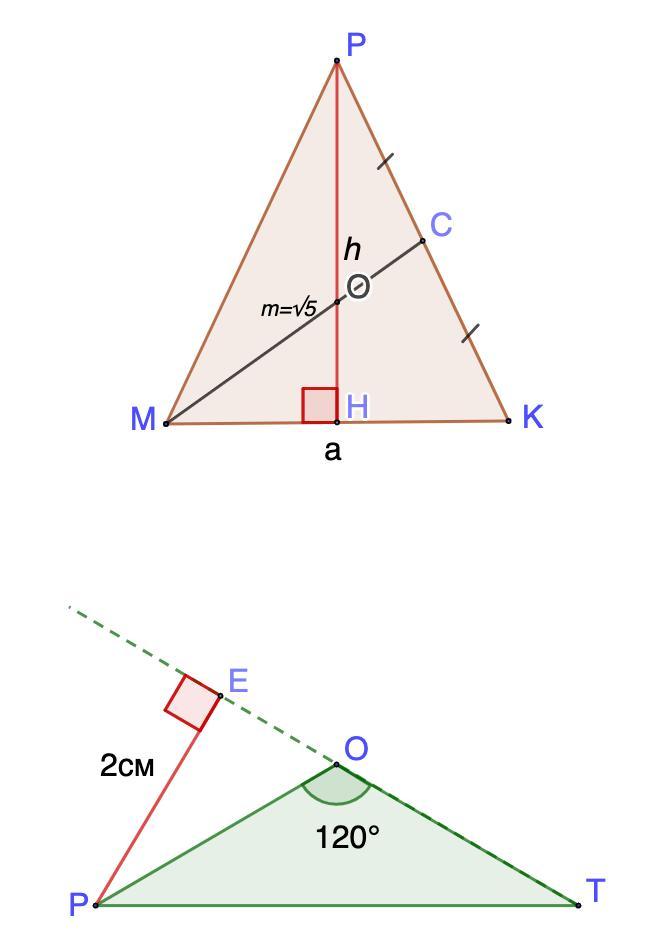
19.15, 19.16 с объяснением​

Answer 1

Ответ:

19.15. Квадрат длины основания равен 8 или 8/9;

19.16. Длина основания равна 4 см

Объяснение:

19.15. Найдите квадрат длины основания равнобедренного треугольника площади S = 2, если длина его медианы, опущенной на боковую сторону равна m = √5.

19.16. Найдите длину основания равнобедренного треугольника, у которого длина высоты, опущенной на боковую сторону равна h = 2см, а угол при вершине равен α = 2π/3.

19.15. Дано: ΔМРК - равнобедренный;

МК - основание; МС = m = √5 - медиана;

S(МРК) = 2;

Найти: МК²

Решение:

Проведем высоту РН.

Обозначим РН - h; MK - a.

• Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.

⇒ S(МРК) = 1/2 · ah

2 = 1/2 ah   ⇒   h = 4/a

• В равнобедренном треугольнике высота, проведенная к основанию, является медианой.

⇒ МН = НК = а/2

• Медианы треугольника пересекаются в одной точке и делятся этой точкой на две части в отношении 2:1, считая от вершины.

⇒ MO : OC = PO : OH = 2 : 1

OH = h/3 = 4/3a;   MO = 2m/3 = 2√5/3

Рассмотрим ΔМОН - прямоугольный.

• Теорема Пифагора:
• Квадрат гипотенузы равен сумме квадратов катетов.

⇒ МО² = ОН² + МА²

$\displaystyle \frac{20}{9}=\frac{16}{9a^2} +\frac{a^2}{4} \;\;\;\;\;|\cdot36a^2;\;\;\;a\neq 0\\\\80a^2-64-9a^4 = 0;\;\;\;\;\;a^2=k$

$\displaystyle 9k^2-80k+64=0\\\\\sqrt{D}=\sqrt{6400-2304}=\sqrt{4096}=64\\ \\ k_1=\frac{80+64}{18}=8;\;\;\;\;\;k_2=\frac{80-64}{18}=\frac{8}{9}$

a² = 8   или   а² = 8/9

19.16. Дано: ΔРОТ - равнобедренный;

РТ - основание;

∠РОТ = 2π/3

РЕ = 2 см - высота

Найти: РТ

Решение:

∠РОТ = 2π/3 = 120° - тупой.

⇒ основание высоты лежит на продолжении ОТ.

Рассмотрим ΔРОТ - равнобедренный.

∠РОТ = 120°

• Сумма углов треугольника равна 180°.

⇒ ∠ОРТ + ∠ОТР = 180° - 120° = 60°

• Углы при основании равнобедренного треугольника равны.

∠ОРТ = ∠ОТР  = 60° : 2 = 30°

Рассмотрим ΔРЕТ - прямоугольный.

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ РТ = 2 РЕ = 4 см