Предмет: Геометрия,
автор: zotova0000
ГЕОМЕТРИЯ! СРОЧНО НУЖНА ПОМОЩЬ!
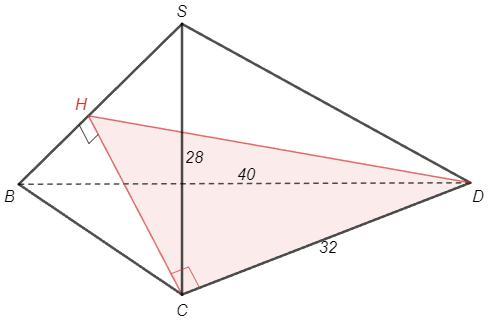
В основании пирамиды SABC лежит прямоугольный треугольник BCD, в котором угол C = 90°, BD = 40, CD = 32. Высота пирамиды SC равна 28. Найдите площадь сечения пирамиды, проходящего через больший катет основания перпендикулярно к среднему боковому ребру. (При выполнении задания необходимо сделать рисунок).
Ответы
Автор ответа:
1
По т Пифагора BC=24
CD - больший катет основания.
SC - высота, т.е. SC⊥(BCD) => SC⊥BC, SC⊥CD
Рассмотрев прямоугольные треугольники SCB и SCD, видим, что
SB - среднее боковое ребро.
Проведем CH⊥SB
CD⊥BC, CD⊥SC => CD⊥(SCB)
CD⊥(SCB), CH⊥SB => DH⊥SB (т о трех перп)
SB⊥CH, SB⊥DH => SB⊥(HCD)
△HCD - искомое сечение
Треугольник SCB: CH - высота из прямого угла
CH =BC*SC/SB =BC*SC/√(BC^2+SC^2) =4 *6*7/√(36+49) =168/√85
CD⊥(SCB) => ∠HCD=90
S(HCD)=1/2 CH*CD =1/2 *168/√85 *32 =2688/√85
Приложения:
Похожие вопросы
Предмет: Биология,
автор: olya2415cl
Предмет: Українська мова,
автор: mmarina44
Предмет: Математика,
автор: belikstalu
Предмет: Русский язык,
автор: okeanmelisa