Question

17. дано функцію: h(x) = (x-2)^2+1

Перед вами кілька тверджень, напишіть щодо них правда/неправда й обґрунтуйте.
А. Наступна нерівність (x-2)^2+1>0 відбудеться для всіх x. Поясніть свій вибір, використовуючи дві причини, принаймні.
Б. Вершина функції максимуму та її показники (2,1).
В. Пряма 3 = y перетинає графік функції рівно у 2 точках.

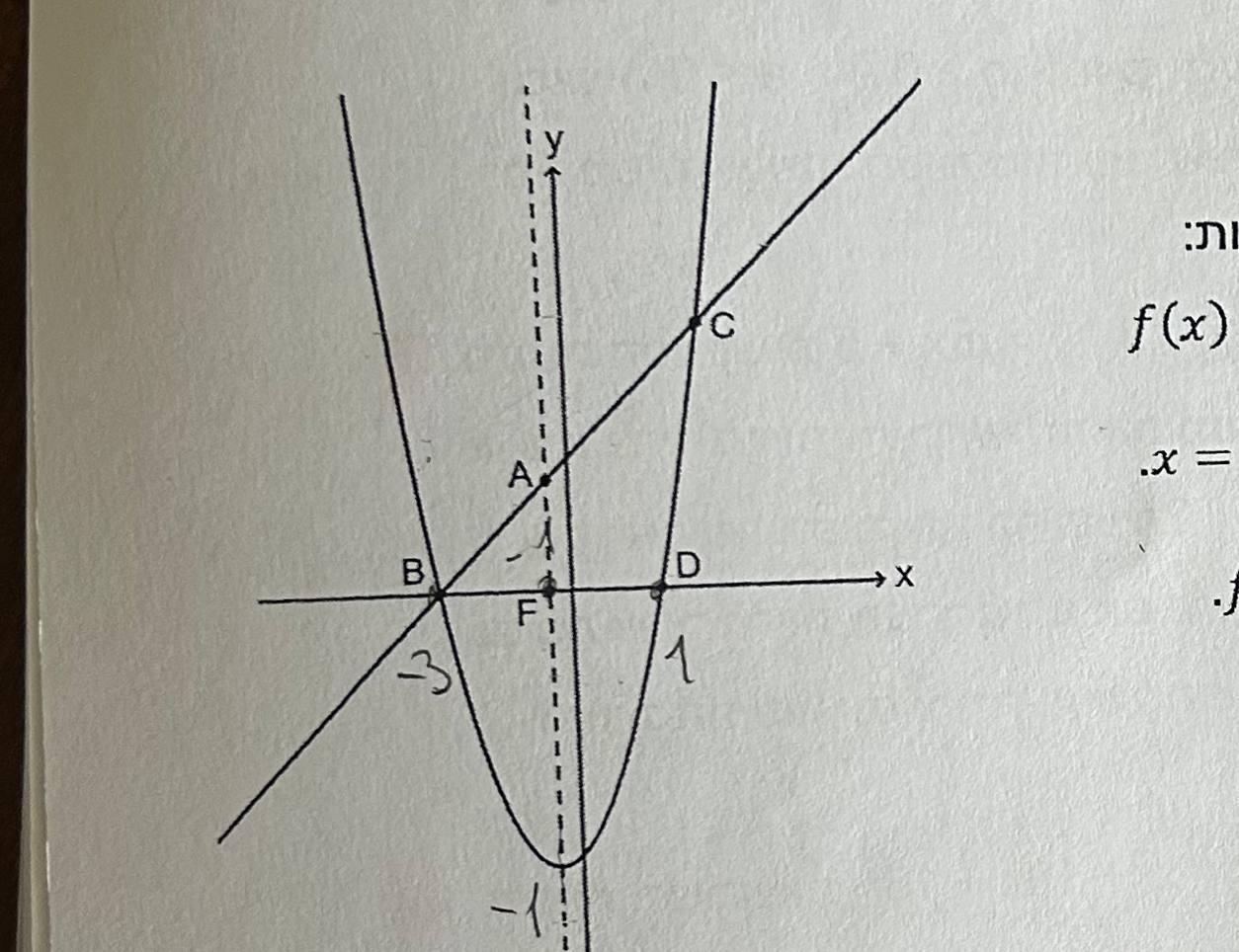
18. На малюнку перед вами графіки функцій: f(x) = (x - b)(x+3), g(x)=x+3.

Дано: вісь симетрії функції f(x) це x=-1

a. Знайдіть параметр b і напишіть функцію f(x)
Б. Напишіть точки B, D, C.
Г. Перелічіть області, у яких f(x) < g(x)
Д. Вісь симетрії перетинає функцію (g)x у точці A і вісь x у точці F (дивіться рисунок).
Д1. Трикутник ABF рівнобедрений? Обґрунтуйте своє твердження.
Д2. Трикутник BAD рівнобедрений? Обґрунтуйте своє твердження.
Е. Точка P знаходиться на графіку функції g(x) і точка R знаходиться на осі симетрії, так що: трикутник AARP ~ трикутник AAFB. Знайдіть точки P, R
*фото до 18 завдання*

Answer 1

Ответ:

17.   Задана функция   $\bf h(x)=(x-2)^2+1$   .

А.  Неравенство   $\bf (x-2)^2+1 > 0$   верно при любых значениях переменной :   $\bf x\in (-\infty ;+\infty \, )$  , так как   $\bf (x-2)^2\geq 0$  при всех  х , и если рассматривать сумму неотрицательного выражения и положительного числа 1  в левой части неравенства , то сумма будет положительной .

Вторая причина.  Графиком функции является парабола с ветвями, направленными вверх , и вершиной в точке ( 2 ; 1 ) . Значит парабола не пересекает ось ОХ, а лежит выше неё в верхней полуплоскости , где  $\bf h(x) > 0$  .

Б.  Вершина параболы в точке ( 2 ; 1 ) . В ней нет максимума, а достигается минимум функции h(x) .  Минимум функции равен  1 .

В.  Прямая  у = 3 пересекает график функции  h(x)  в двух точках , так как область значений функции :  $\bf h(x)\in [\ 1\ ;+\infty )$  , a  3 > 1 .

18.   Заданы функции  :   $\bf f(x)=(x-b)(x+3)\ ,\ \ g(x)=x+3$  .

Ось симметрии функции f(x) - это прямая  x  = -1 .  

A)  Значит вершина параболы  f(x)  имеет абсциссу  х₀ = -1 .

Абсциссу вершины параболы находим по формуле   $\bf x_0=-\dfrac{b}{2a}$   .

$\bf (x-b)(x+3)=x^2+3x-bx-3b=x^2+(3-b)\, x-3b\ \ ,\ \ a=1\\\\x_0=-\dfrac{3-b}{2a}=-1\ \ \Rightarrow \ \ \ -3+b=-2a\ \ ,\ \ b=-2\cdot 1+3=-2+3=1$  

Тогда уравнение параболы имеет вид  $\bf f(x)=x^2+2x-3$   .

Б.  Координаты точек В и D  находим как координаты точек пересечения параболы и оси ОХ .

$\bf x^2+2x-3=0\ \ ,\ \ x_1=-3\ ,\ x_2=1$  (по теореме Виета)

Точки  $\bf B(-3\, ;\, 0\, )\ ,\ \ D(\, 1\, ;\, 0\, )$  

Координаты точки С находим как координаты точки пересечения параболы f(x) и прямой g(x) .

$\bf x^2+2x-3=x+3\ \ \Rightarrow \ \ \ x^2+x-6=0\ \ ,\ \ x_1=-3\ ,\ x_2=2\\\\g(2)=2+3=5$  

Точка  $\bf C(\, 2\, ;\, 5\, )$  .

Г.  $\bf f(x) < g(x)$   при   $\bf x\in (-3\, ;\, 2\, )$  .

Д. Точка пересечения прямой  х = -1  и функции  g(x) - точка  А(-1 ; 2)

Точка пересечения прямой  х = -1  и оси ОХ - точка  F(-1 ; 0 )  .

Д1.  ΔАBF - равнобедренный , так как  $\bf BF=AF=2$  .

Д2.  ΔBDA - равнобедренный , так как  $\bf AB=AD$  .

$\bf AB=\sqrt{(-3+1)^2+(0-2)^2}=\sqrt{4+4}=2\sqrt2\\\\AD=\sqrt{(-1-1)^2+(2-0)^2}=\sqrt{4+4}=2\sqrt2$  

Е.  Точка Р находится на прямой g(x)=x+3 , а точка R находится на прямой  х = -1 . Причём  ΔARP ~ ΔAFB  .

Можно, например, взять точки R( -1 ; 6 ) и P(3 ; 6 ) . Тогда указанные треугольники будут подобны по двум углам .

Если записать в общем виде, то точки  Р и  R будут иметь координаты :   R( -1 ; a )  ,  P( a-3 ; a )  , где  а = const .