Помогите решить 2 задачи по середине

Ответы
Ответ:
280 ÷ 1,7 = 2800/17 ≈ 165 (р) - цена килограмма изюма
130 ÷ 1,3 = 100 (р) - цена килограмма яблок
360 ÷ 2 = 180 (р) - цена килограмма черносливов
165 + 100 + 180 = 445 (р.) - стоимость всех сухофруктов в количестве 1 кг
Ответ: 445 р.
второе не знаю как решать, потому что у меня вышло больше чем 280 рублей
Ответ:
1) Стоимость купленных сухофруктов составила
1,7·280 + 1,3·130 + 2·360 = 476 + 169 + 720 = 1365 (руб.)
Всего куплено 1,7 + 1,3 + 2 = 5 кг сухофруктов .
Средняя стоимость 1 кг сухофруктов равна 1365 : 5 = 273 (руб.)
б) В дополнение купили груши по цене 330 руб за 1 кг . Стоимость смеси составила 280 руб. за 1 кг .
Пусть купили х кг груш, тогда стоимость смеси за 1 кг будет равна
(1365 + 330х)/(5+х) = 280 ⇒ 1365+330х = 280(5+х) ,
330х - 280х = 1400 - 1365 , 50х = 35 , х = 0,7
Купили 0,7 кг груш .
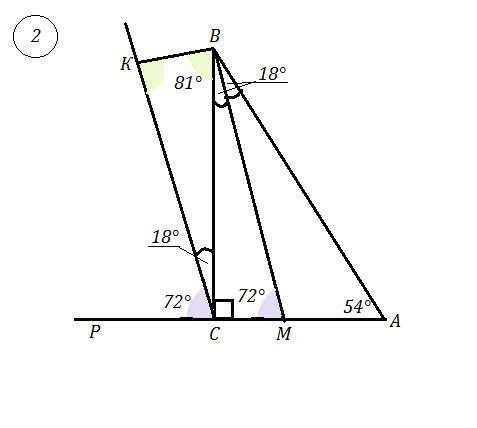
2) Дан ΔАВС ,
∠А : ∠В : ∠С = 3 : 2 : 5 ⇒ ∠А = 3х° , ∠В = 2х° , ∠С = 5х° ⇒
3х°+2х°+5х°=180° , 10х° = 180° ⇒ х° = 18°
Значит ∠А=3·18° = 54° , ∠В = 2·18° = 36° , ∠С = 5·18° = 90°
Биссектриса ВM делит ∠В пополам , поэтому
∠ABM = ∠CBM = 36° : 2 = 18°
Получаем, что в ΔCВM есть ∠СBM = 18° и ∠BСM = 90° , значит ΔCВМ прямоугольный . Третий угол этого треугольника равен ∠BMC = 180° - 90° - 18° = 72° .
Луч CK || BM . Продлим сторону АС за точку С , поставим точку Р . Получим , что ∠КСР = ∠ВМС = 72° как соответственные углы при параллельных прямых СК и ВМ и секущей АР .
∠BСР = 90° , так как ∠BСM = 90° .
∠ВСР = ∠КСР + ∠ВСК = 72° + ∠ВСК = 90°
∠ВСК = 90° - ∠КСР = 90° - 72° = 18°
Так как по условию ВС=СК , то ΔВСК - равнобедренный . Угол при его вершине равен 18° . А углы при основании равны . Значит,
∠ВКС = ∠КВС = ( 180° - 18° ) : 2 = 81°
∠МВК = ∠КВС + ∠МВС = 81° + 18° = 99°