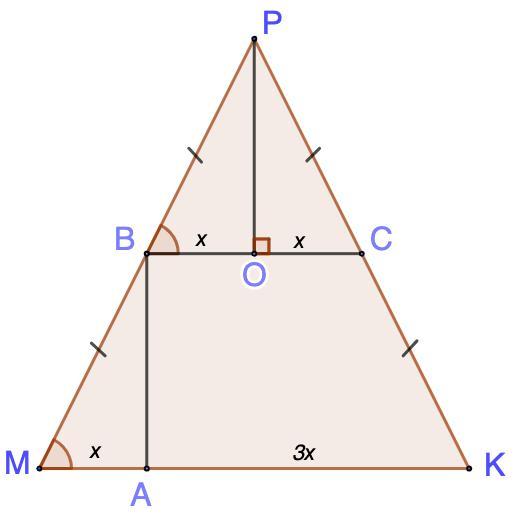
3. Деяка пряма, що паралельна основі МK рівнобедреного трикутника МРK,
перетинає сторони МР і РK у точках В і С відповідно. Точка А ділить відрізок
МK у відношенні 1:3, рахуючи від точки М; ВС=2АМ. Знайдіть <МАВ.
Ответы
Ответ:
∠МАВ = 90°
Объяснение:
3. Некоторая прямая, параллельная основанию МК равнобедренного треугольника МРК, пересекает стороны МР и РК в точках В и С соответственно. Точка А делит отрезок МК в отношении 1 : 3, считая от точки М; ВС=2 АМ. Найдите ∠МАВ.
Дано: ΔМРК - равнобедренный;
МК - основание;
ВС ∩ МР = В; ВС ∩ РК = С
ВС || МК;
А ∈ МК; АМ : АК = 1 : 3;
ВС = 2 АМ
Найти: ∠МАВ
Решение:
АМ : АК = 1 : 3
Пусть АМ = х, тогда АК = 3х, а МК = 4х.
Рассмотрим Δ МРК - равнобедренный.
ВС || МК; ВС = 2 АМ = 2х = 1/2 МК
- Если отрезок параллелен стороне треугольника и равен его половине, то отрезок является средней линией.
⇒ ВС - средняя линия ΔМРК.
⇒ МВ = ВР = РС = СК
- В ΔВРС проведем высоту РО.
Рассмотрим ΔВРС - равнобедренный.
- В равнобедренном треугольнике высота, проведенная к основанию, является медианой.
⇒ ВО = ОС = х
Рассмотрим ΔМВА и ΔВРО.
МВ = ВР
МА = ВО = х
∠ВМА = ∠РВО (соответственные при ВС || МК и секущей МР)
⇒ ΔМВА = ΔВРО (по двум сторонам и углу между ними, 1 признак)
⇒ ∠МАВ = ∠ВОР = 90° (как соответственные элементы)
#SPJ1