Предмет: Математика,
автор: Fake123
Решить 2 задания по математике
Приложения:


Ответы
Автор ответа:
2
Ответ:
1) Ряд Маклорена для функции y = cosx .
Заменим в этой формуле х на х²/4 , получим
Вычислим интеграл .
Достаточно взять два слагаемых для подсчёта суммы с точностью до 0,001 , так как уже третье слагаемое по модулю меньше заданной точности , | 0,00002 | < 0,001 . Промежуточные вычисления проводим до 4-го знака (один запасной знак) после запятой , а ответ округляем до 3-го знака после запятой .
Ответ: 0,994 .
2) Найти интервал сходимости ряда .
Применим признак Даламбера к ряду, составленному из абсолютных величин членов исходного ряда .
Чтобы ряд сходился , надо чтобы выполнялось неравенство
Интервал сходимости : .
Приложения:


fizikyadershik68:
Здравствуйте, благодарю вас за красивое решение. С уважением, Владимир.
Здравствуйте, спасибо .
Автор ответа:
0
Пошаговое объяснение:
Ответ смотрите на фотографии.
Приложения:

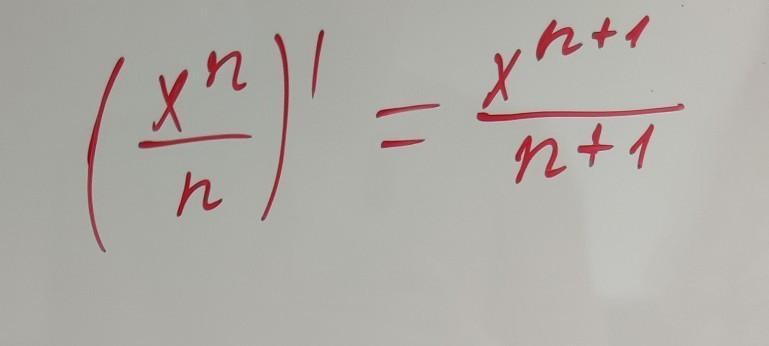



Здравствуйте, феноменальное решение. Вы огромный молодец. С уважением, Владимир.
Здравствуйте, спасибо большое.
Похожие вопросы
Предмет: Математика,
автор: zhhxsdjcnd
Предмет: Литература,
автор: nadburmasova
Предмет: Русский язык,
автор: ajzanujym897
Предмет: Химия,
автор: krylovavika4
Предмет: Алгебра,
автор: vkaramshinov