Question

Допоможіть будласка!

Answer 1

Ответ:

63

Объяснение:

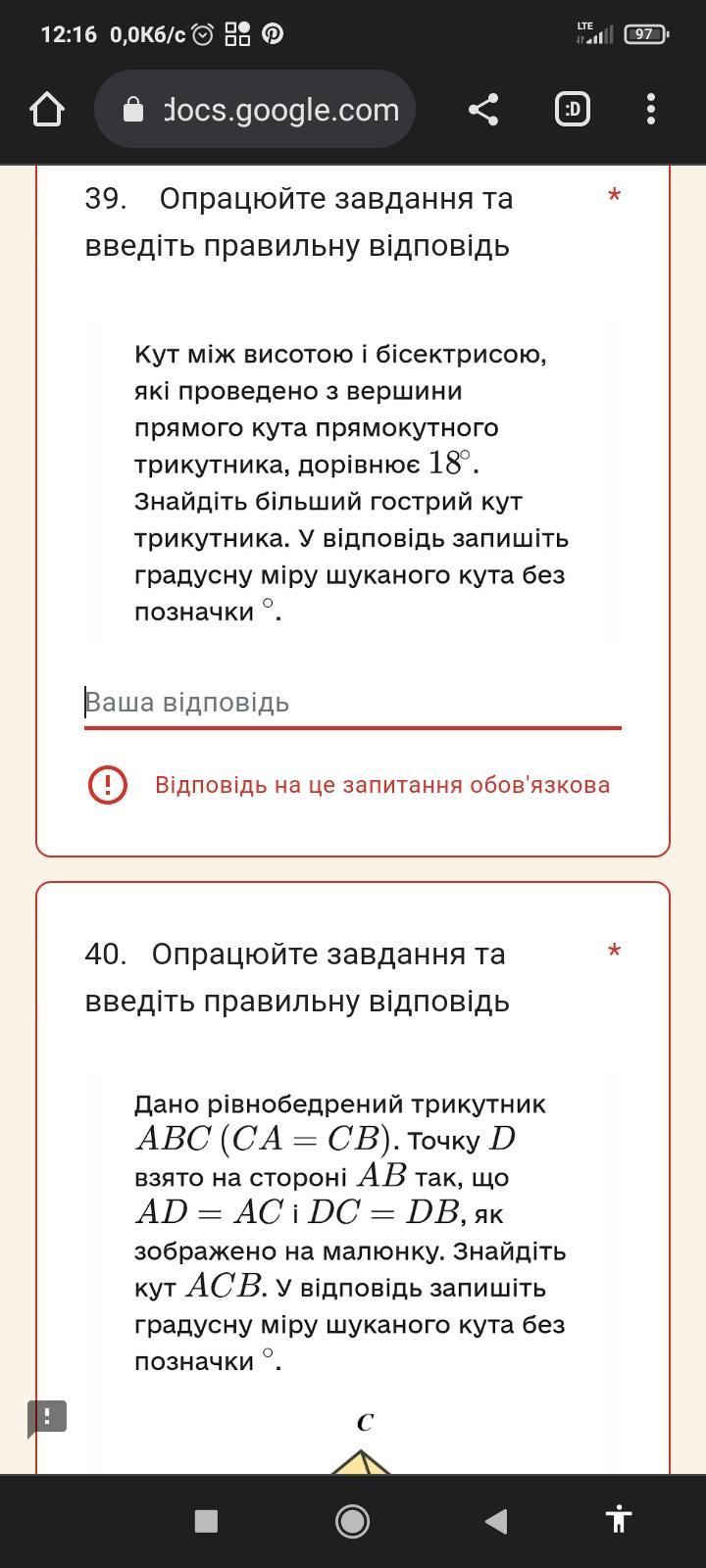
Бісектриса поділяє прямий кут у 90° на дві рівні частини по 45°.

Через одну з цих частин проходить висота трикутника, відділяючи від неї ще 18°. Отже, частина прямого кута, що залишається по інший бік висоти дорівнює 45-18=27°.

У місці перетину з гіпотенузою трикутника висота утворює два прямих кути, адже є перпендикуляром. Отже, утворюється маленький трикутник з кутом 90°, кутом 27° та невідомим кутом з великого трикутника.

Оскільки сума кутів в трикутнику завжди дорівнює 180°, невідомий кут 180°-90°-27°=63°.

Інший кут великого трикутника дорівнює 180°-90°-63°=27°.

Answer 2

Ответ:

63

Объяснение:

Рассмотрим Δ AHD:

∠AHD=90° (так как AH - высота);

∠HAD=18° (по условию);

∠AHD+∠HAD+∠ADH=180° (по теореме о сумме углов в треугольнике)

⇒ ∠ADH=180°-∠AHD-∠HAD=180°-90°-18°=72°

Рассмотрим Δ BAD:

AD - биссектриса (по условию) ⇒ ∠BAD=CAD=90°:2=45°;

∠ADB=72° (из решения выше);

∠ABD+∠BAD+∠ADB=180° (по теореме о сумме углов в треугольнике)

⇒ ∠ABD=180°-∠ADB-∠BAD=180°-72°-45°=63°

Рассмотрим Δ ABC:

∠BAC=90° (так как Δ ABC - прямоугольный);

∠ABC=63° (из решения выше);

∠ABC+∠BAC+∠ACB=180° (по теореме о сумме углов в треугольнике)

⇒ ∠ACB=180°-∠ABC-∠BAC=180°-63°-90°=27°

Острые углы - ∠ABC=63° и ∠ACB=27°

63°>27° ⇒ ∠ABC>∠ACB

Ответ: 63.