Question

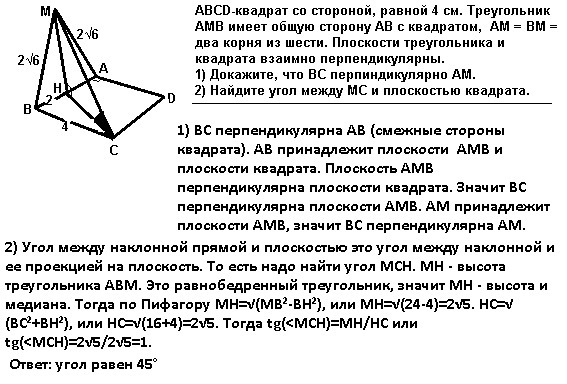
Рисунок задачи пожалуйста!!!  ABCD-квадрат со стороной, равной 4 см. Треугольник AMB имеет общую сторону AB с квадратом,  AM = BM = два корня из шести. Плоскости треугольника и квадрата взаимно перпендикулярны.
1) Докажите, что BC перпиндикулярно AM.
2) Найдите угол между MC и плоскостью квадрата. 

Answer 1

1) ВС перпендикулярна АВ (смежные стороны квадрата). АВ принадлежит плоскости  АМВ и плоскости квадрата. Плоскость АМВ перпендикулярна плоскости квадрата. Значит ВС перпендикулярна плоскости АМВ. АМ принадлежит плоскости АМВ, значит ВС перпендикулярна АМ.
2) Угол между наклонной прямой и плоскостью это угол между наклонной и ее проекцией на плоскость. То есть надо найти угол МСН. МН - высота треугольника АВМ. Это равнобедренный треугольник, значит МН - высота и медиана. Тогда по Пифагору МН=√(МВ²-ВН²), или МН=√(24-4)=2√5. НС=√(ВС²+ВН²), или НС=√(16+4)=2√5. Тогда tg(<МСН)=МН/НС или tg(<МСН)=2√5/2√5=1.
Ответ: угол равен 45°.