Предмет: Алгебра,
автор: Аноним
вибачаюсь рівень студентський,мабуть не на те натиснула.допопможіть будь ласка,в мене є три години)Скласти рівняння дотичної до кривої у точці, що відповідає значенню параметра t=t0.
Приложения:
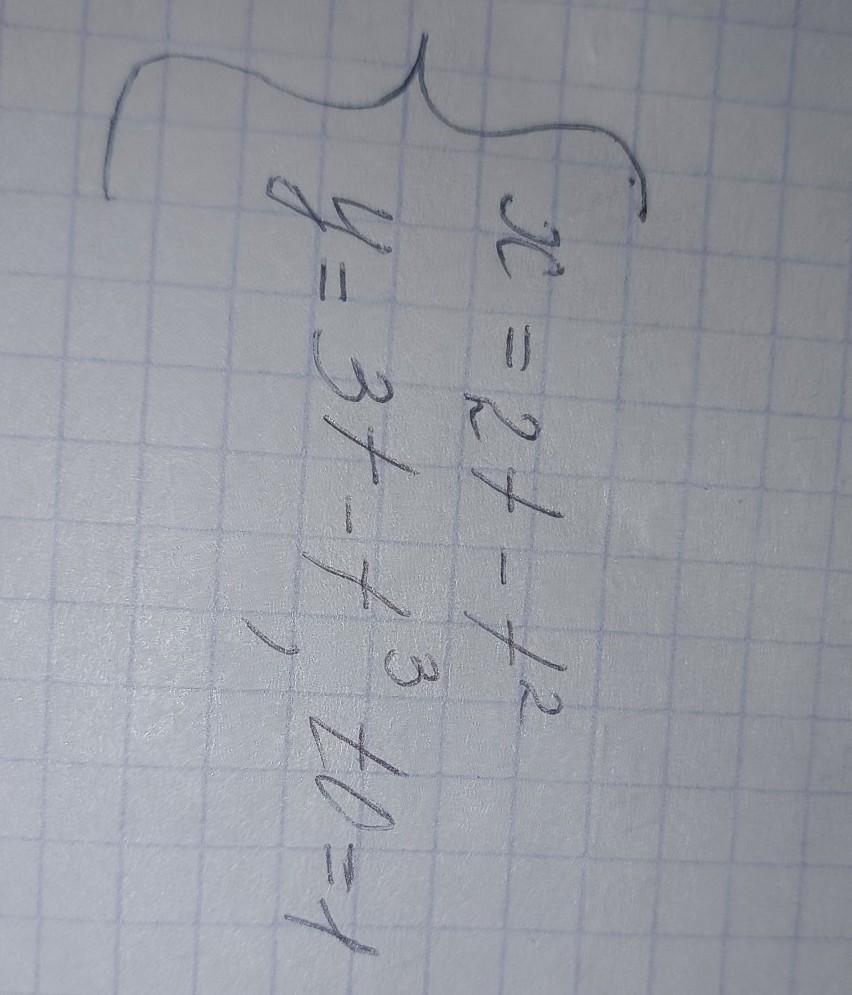
Ответы
Автор ответа:
3
Ответ:
Уравнение касательной: у = 3х - 1.
Объяснение:
Составить уравнение касательной.
, t₀ = 1
- Уравнение касательной:
t₀ = 1
Тогда
Найдем производную:
x₀ = 1
⇒
y₀ = 2; y'₀ = 3; x₀ = 1
Составляем уравнение касательной:
y = 2 + 3(x - 1) = 2 + 3x - 3 = 3x - 1
Уравнение касательной: у = 3х - 1.
Похожие вопросы
Предмет: Литература,
автор: mazzafackersha560
Предмет: Математика,
автор: milazlaq
Предмет: История,
автор: kavalchukillia11
Предмет: Геометрия,
автор: dannyelpaze
Предмет: Русский язык,
автор: rustamsitdikov2020