Question

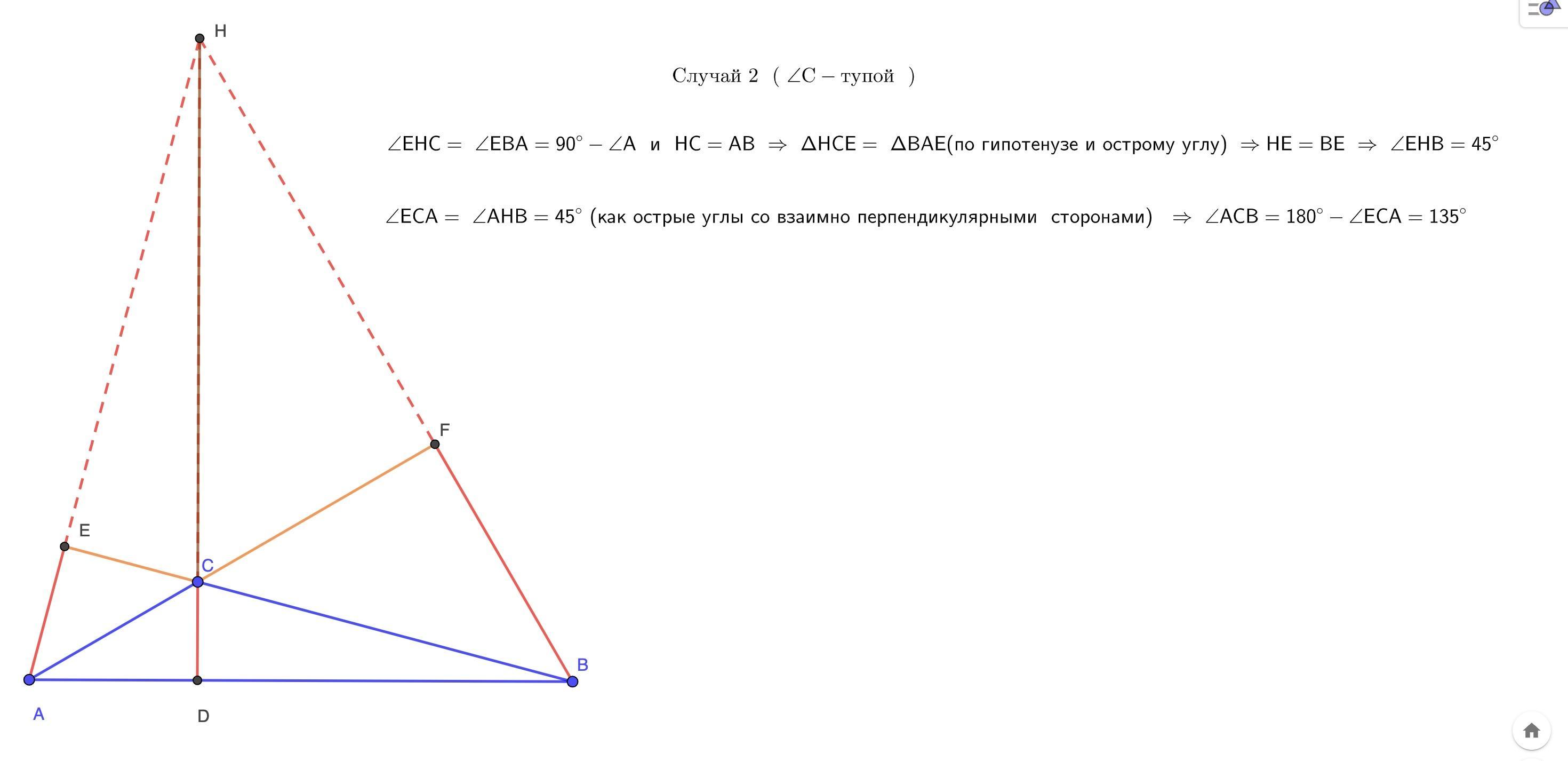
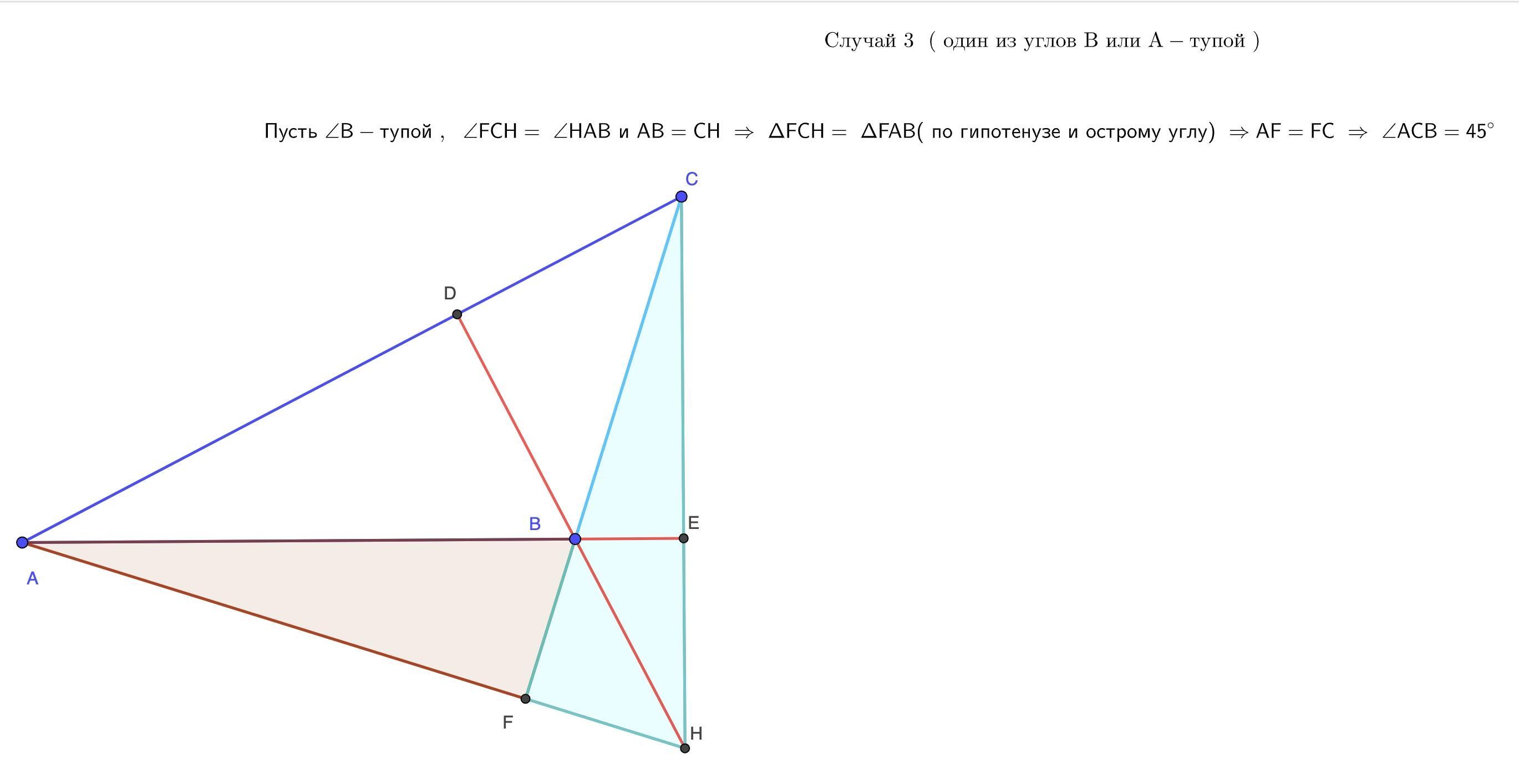
У трикутнику ABC прямі, що містять його висоти, перетинаються в точці H . Відомо, що HC = AB . Знайдіть величину кута ACB .

Answer 1

Ответ:

45°

Объяснение:

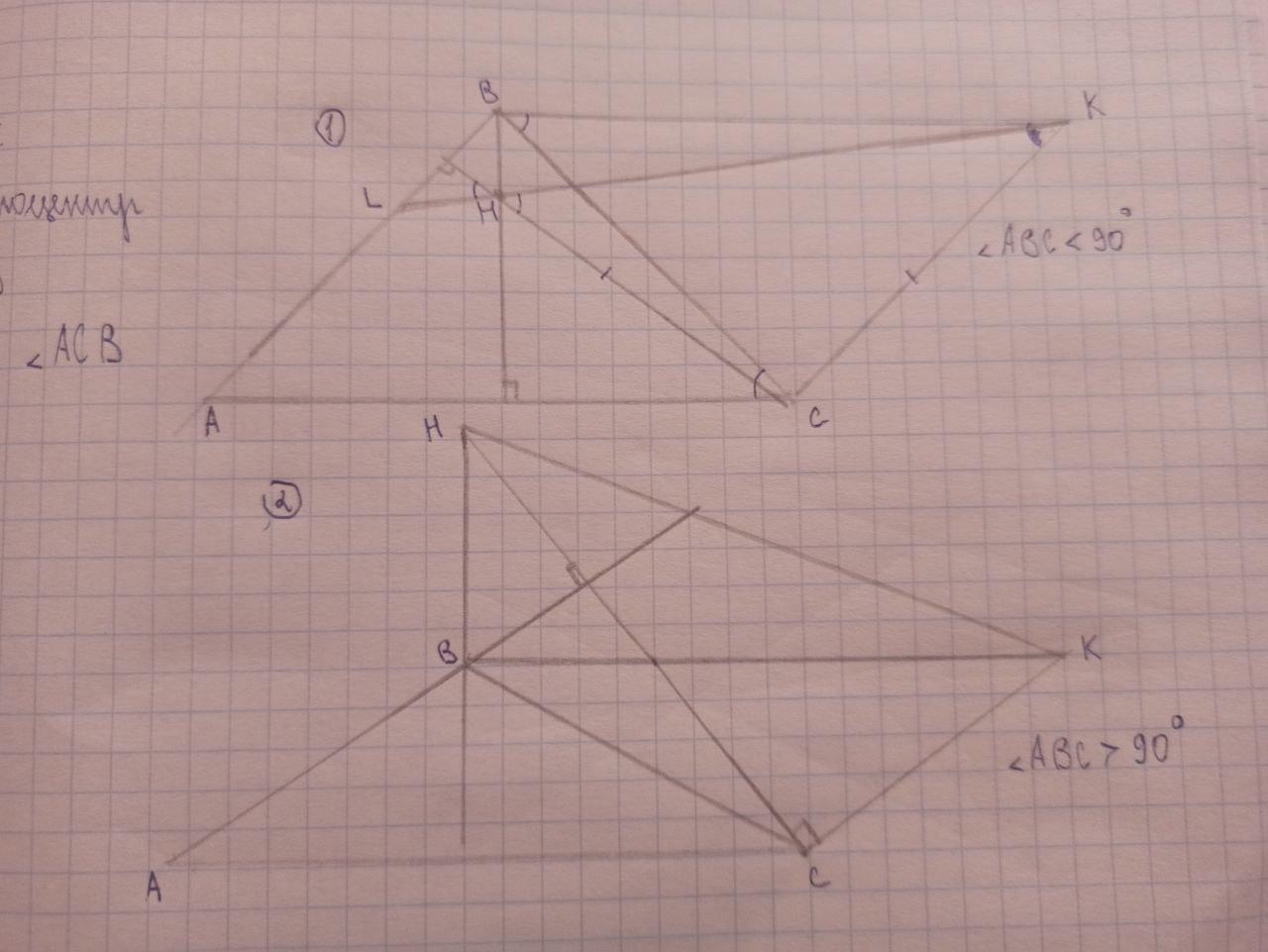
Будет рассмотрено два случая, которые изображены на фото, но отрезок CK=AB, CK║AB будет проведён в каждом случае, тем самым будет образован параллелограмм ABKC.

Случай 1(риснок 1).

1) Так как ΔHCK-равнобедренный, то ∠СHK=∠CKH.

2) Продлим HK до пересечения с AB в допустим точке L. ∠BLK=90°-∠KHC=90°-∠HKC. Но с другой стороны ∠BLK=∠HKC как накрест лежащие. Два таких равенства может выполняться одновременно только при ∠HKC=45°

3) ∠HCK=180°-45°×2=90°. ∠HBK=90° ⇒ HBKC-вписанный и ∠CBK=∠CHK=45°(опираются на одну дугу). ∠CBK=∠ACB=45°(накрест лежащие)

Случай 2(рисунок 2).

1) На рисунке отмечено два прямых угла: один по условию, другой равен ему как накрест лежащий, поскольку ΔHCK-р/б, то ∠CHK=∠CKH=(180°-90°)/2=45°.

2)∠HBK=90°, ∠HCK=90°, углы опираются на одну сторону ⇒ BHKC-впис. ⇒ ∠СHK=∠CBK=45°(опираются на одну дугу)

3)∠CBK=∠ACB=45°(накрест лежащие).

Answer 2

Ответ:

45° или  135° ......................................

Объяснение: