Предмет: Геометрия, автор: littlegvyntik

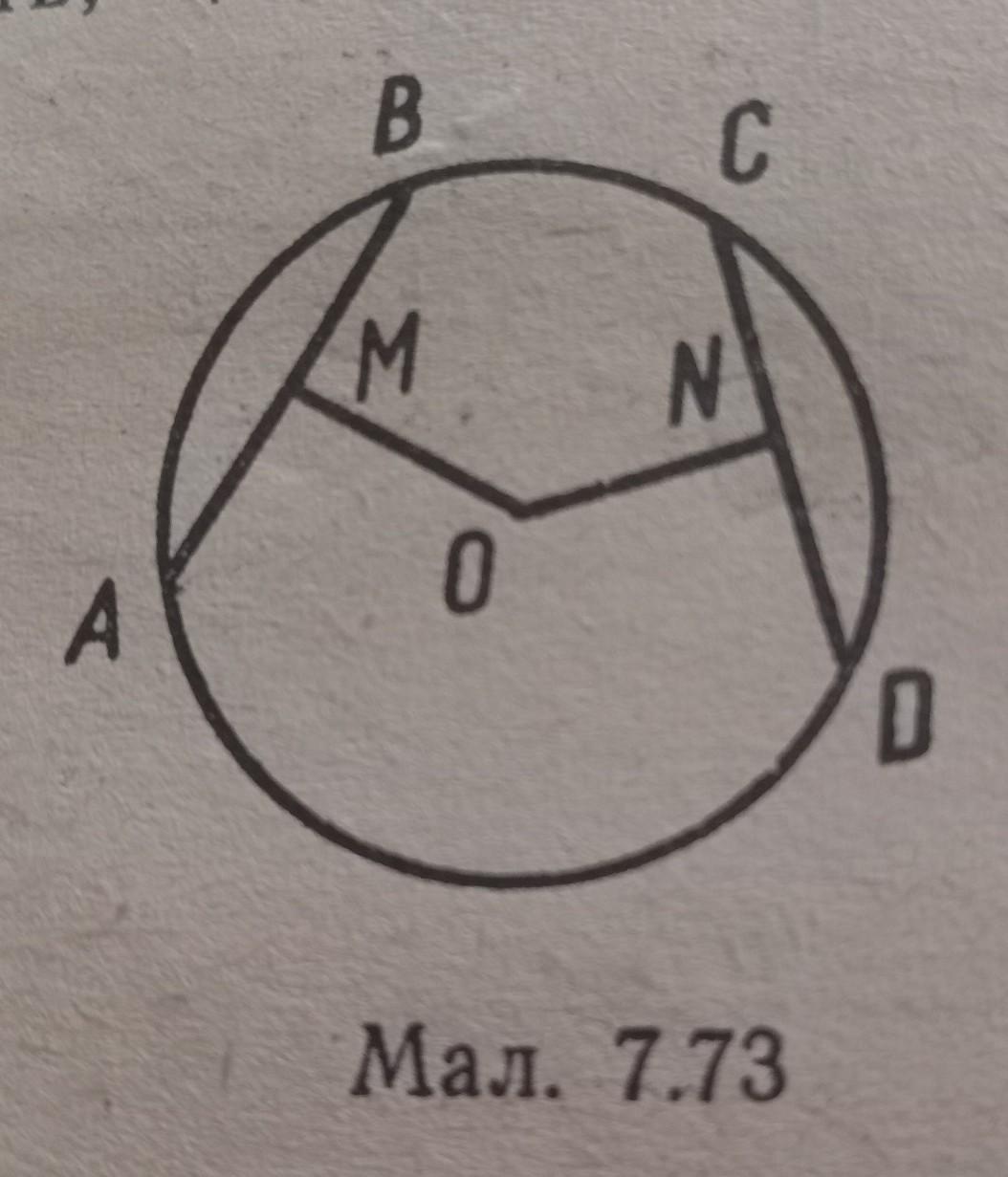
Дано: AB=CD, OM перпендикулярно AB, ОN перпендикулярно CD.
Довести: ОM=ON
​

Приложения:
hderyb: если отрезок из центра перепендикулярен хорде, то он делит его пополам. BM=CN, OB=OC(радиусы) и два прямых угла дают равенство треугольников OMB и OCN а значит и OM и ON

Ответы

Автор ответа: dobra888
1

Відповідь:

Пояснення:

Проведемо радіуси до кінців відрізків AB  i  CD .  За ІІІ ознакою

рівності тр - ників ΔАОВ = ΔCOD , бо АВ = CD - за умовою ;

ОА = ОС  i  OB = OD як радіуси одного кола . Звідси ∠ОАМ = ∠ОСN.

Як відомо OM  i  ON - серединні перпендикуляти до рівних хорд

AB  i  CD , тому AM = CN . Тому за  І ознакою рівності тр - ників

ΔАОМ = ΔCON . Звідси OM = ON  як відповідні сторони .  

Предыдущий вопрос
Следующий вопрос
Похожие вопросы
Предмет: Литература, автор: 8bkqsn4c4z
Скласти байку,невелику
2 года назад
Предмет: Химия, автор: rozag8970
Дати відповіді на тести:
1. Вибрати з наступних матеріалів розчин:
а) сталь; б) дистильована вода;
в) глина; г) морська вода.
2. За агрегатним станом розчин може бути?
а) рідкий; б) ненасичений;
в) колоїдний; г) істинний.
3. За розміром частинок дисперсної фази розчин може бути:
а) рідкий; б) ненасичений;
в) газоподібний; г) істинний.
4. Розчин, в якому речовина при певній температурі більше не розчиняється,
називають:
а) насичений; б) ненасичений;
в) розведений; г) пересичений.
5. В шлунковому соку розчиненою речовиною буде:
а) соляна кислота; б) натрій гідроксид;
в) вода; г) сірчана кислота.
6. Яка речовина буде розчинятись в воді?
а) золото; б) нафта;
в) глюкоза; г) целюлоза.
7. Яка сіль буде нерозчинна в воді?
а) K2SO4; б) NaCl;
в) BaSO4; г) FeCl3.
8. Щоб збільшити розчинність газу, треба:
а) понизить температуру; б) підвищити температуру;
в) підвищити тиск; г) понизить тиск.
9. При збільшенні температури, розчинність речовини:
а) зменшується; б) збільшується;
в) не змінюється; г) спочатку збільшується, а потім
зменшується.
10. Тиск впливає на розчинність речовини:
а) рідкої; б) твердої;
в) газоподібної; г) нерозчинної.
2 года назад
Предмет: Українська мова, автор: mykytakatz
Складіть 3 сурядних ускладнених реченні і зробіть морфологічний розбір
2 года назад
Предмет: Английский язык, автор: danuskor2020
Fill in the gaps with some, any, one, somebody, someone, anybody, anyone, something, anything where necessary.
1. There are cakes on the plate.
2. There aren't children in the schoolyard.
3. Does know how to solve this task?
4. Are there shopping centres here? — Yes, there are
5. I'm in a hurry. Give me shirt.
6. Is there in the fitting room? — Yes, there is
7. Do you like soft cheeses? — No, 1 prefer hard
8. I can't see on t[4? shelf.
9. Where can I buy needles and thread?
10. Take my pen. - Thank you, I have
7 лет назад
Предмет: Физика, автор: saifmayar10
При измерении пульса человека было зафиксировано 75 пульсаций крови за 1 минуту. Определите частоту сокращения сердечной мышцы.
7 лет назад