Предмет: Алгебра,
автор: Аноним
Решите пожалуйста срочно
Номер 29 и 30
Приложения:
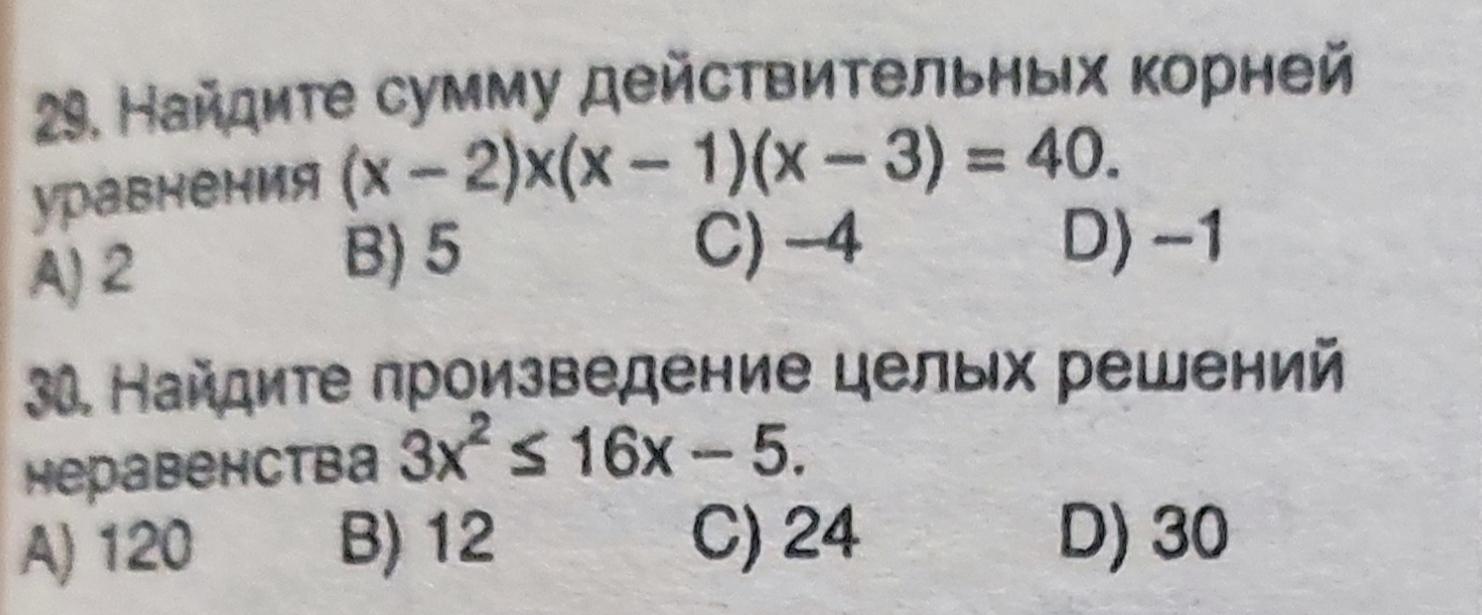
ВикаБач:
Теорема Виета
Ответы
Автор ответа:
1
Ответ:
29) Найти сумму действительных корней уравнения
Замена :
Cделаем обратную замену .
Получим два комплексных корня .
Получим два действительных корня .
Сумма действительных корней равна
30) Найти произведение целых решений неравенства .
Тогда неравенство можно записать в виде
Решаем неравенство методом интервалов . Найдём знаки функции в интервалах : .
Решение неравенства : .
Целые решения неравенства :
Произведение целых решений :
Ответ: А) .
Приложения:



29 Не нужно находить корни! Это теорема Виета. Сумма =3 (-коэффициент при х в квадратном уравнении с D > 0).
Похожие вопросы
Предмет: Английский язык,
автор: lusjannyak21
Предмет: Алгебра,
автор: kindzerskamariana
Предмет: Литература,
автор: HEJXHDNE
Предмет: Математика,
автор: Sergejj77
Предмет: Немецкий язык,
автор: wander3472