Точки дотику вписаного в трапецію кола ділять одну її бічну сторону на відрізки 9 см і 16 см, а другу – у відношенні 4:9. Знайдіть основи трапеції.
Ответы
Відповідь:
Точка касания вписанной в трапецию окружности делит одну боковую сторону на отрезки 9 см и 16 см, а другую - на отрезки, которые относятся как 4:9. Найти основания трапеции.
Решение:
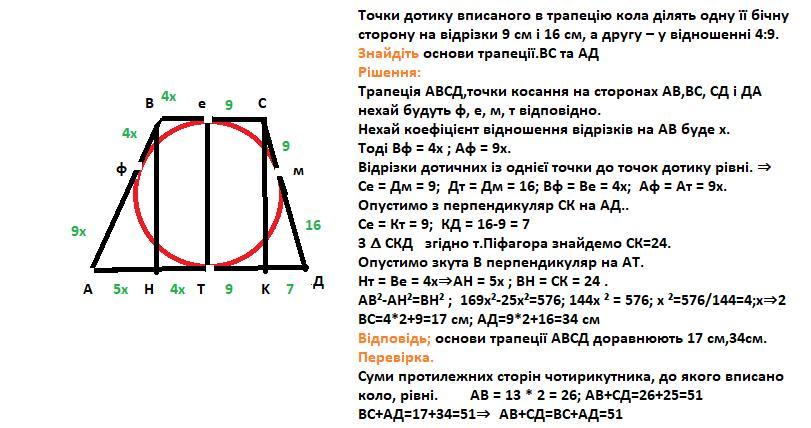
Пусть данная трапеция. АВСД. Точки касания на АВ, ВС, СД и ДА пусть будут ф, е, м, т соответственно.
Коэффициент отношения отрезков на АВ будет х.
Тогда Вф=4х, Аф=9х.
Отрезки касательных из одной точки до точек касания равны. ⇒
Се=См=9; Дт=Дм=16; Вф=Ве=4х; Аф=Ат=9х
Опустим из С перпендикуляр СК на АД.
Се=Кт=9; КД=16-9=7
Из ∆ СКД по теореме Пифагора найдем СК=24.
Опустим из В перпендикуляр на АД.
Нт=Ве=4х⇒ АН=5х; ВН=СК=24 ; АВ²-АН²=ВН²; 169х²-25х²=576;144х²=576; х⇒2
ВС=4*2+9=17 см
АД=9*2+16=34 см
Ответ:основы трапеции АВСД :ВС=17см; АД=34см.
Можно провести проверку правильности решения:
Суммы противоположных сторон четырехугольника, в который вписана окружность. равны.
АВ=13*2=26;АВ+СД=26+25=51; ВС+АД=17+34=51⇒
АВ+СД=ВС+АД=51
Пояснення:
написала на рисунке на украиском языке,а здесь на русском.
Ответ:
17 и 34 ....................................
Объяснение:
