Предмет: Алгебра,
автор: borakvalentina
укажіть найменше ціле число,що є розв'язком нерівності.
Приложения:
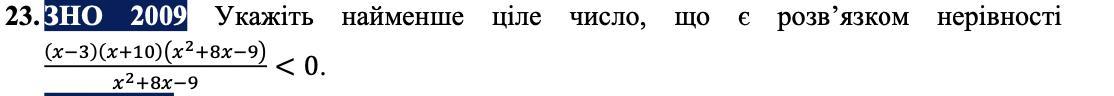
Ответы
Автор ответа:
0
Ответ:
Решить неравенство .
ОДЗ: знаменатель не может быть равен 0 : .
Найдём корни квадратного трёхчлена по теореме Виета :
, так как
.
Дробь имеет одинаковые множители в числителе и в знаменателе . Сократим их , получим
Решим неравенство методом интервалов , учитывая ОДЗ функции .
Знаки:
Выбираем интервалы, где определён знак минус, т.к. неравенство имеет знак "меньше" .
Ответ: .
Наименьшее целое решение неравенства - это х = -8 .
Приложения:

Похожие вопросы
Предмет: Химия,
автор: miliikotik568
Предмет: Биология,
автор: ilonabilogorodska16
Предмет: Українська література,
автор: maksimilianabojko53
Предмет: Другие предметы,
автор: 8914586
Предмет: Русский язык,
автор: vvybor12
Сокращаешь и числитель и знаменатель на x^2+8x-9
Остается (x-3)(x+10). Рассматриваешь два случая, и у тебя выходит (-10;3). В ответе пишешь наименьшее целое число с учетом ОДЗ