Боковая сторона трапеции разделена на пять равных частей, и через третью
точку деления (считая от конца меньшего основания) проведена прямая, параллель
ная основаниям трапеции. Найдите отрезок прямой, заключённый между сторонами
трапеции, если основания трапеции равны a и b и a > b
Ответы
Відповідь: 1/5 (2a + 3b) .
Пояснення:
ABCD - трапеція , в якої BC║AD .
Нехай M – дана точка на cтороні AB (BM : AM = 3 : 2), MN –
шуканий відрізок. Тоді за теоремою Фалеса
CN : DN = BM : AM = 3 : 2.
Проведемо діагональ AC і позначимо через K точку її перетину
із відрізком MN . Из подібності тр - ників CKN і CAD – KN = 3/5 b;
МК = 2/5 а . Тоді шуканий відрізок
MN = MK + KN = 2/5 a + 3/5 b = 1/5 (2a + 3b) .
В - дь : 1/5 (2a + 3b) .
Ответ:
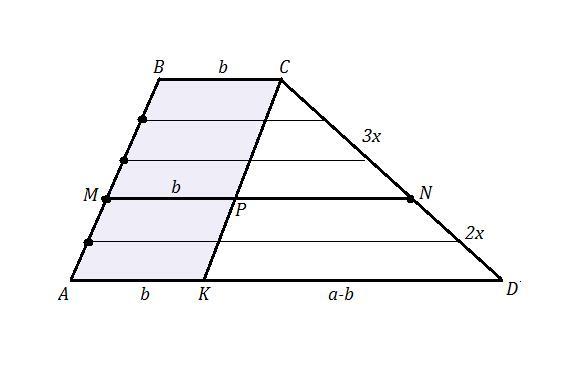
Дана трапеция ABCD . Боковая сторона АВ разделена на 5 равных частей . Проведена прямая MN || AB через третью точку деления, считая от точки В . Основания АD = a , DC=b , a > b . Найти длину MN .
Через вершину C проведём прямую, параллельную боковой стороне AB : CK || AB . Пусть K – точка её пересечения с основанием AD, а точка Р – с отрезком MN .
АВСК - параллелограмм , так как ВС || МР ( MN) и АВ || CK .
AK = BC = b .
Тогда KD = AD - AK = a - b .
Аналогично, МВСР - параллелограмм и ВС = MP = b .
Так как PN || KD (MN || AD ) , то прямая PN отсекает от треугольника CKD подобный треугольник CPN . Это следует из признака подобия по двум углам : ∠СРN = ∠СKD как соответственные углы при параллельных MN и AD и секущей СК , ∠КСD - общий .
CN = 3x , ND = 2x ⇒ CD = 3x+2x = 5x
CN : CD = 3 : 5 ⇒ PN : KD = 3 : 5 ⇒ PN = (3/5 ) · KD = 3/5 · (a-b) .
Значит ,