Предмет: Геометрия, автор: stalskyigleb

У якому відношенні, рахуючи від вершини, треба поділити бічну сторону

трикутника двома прямими, паралельними основі, щоб площа трикутника

була поділена на три рівні частини?

Ответы

Автор ответа: p15

Ответ:

Площадь треугольника равна половине этого основания (которому параллельны две прямые) на опущенную на него высоту. Точно так же с теми треугольниками, которые получатся. Понятно, что все треугольники будут подобны, потому и их боковые стороны и высота будут пропорциональны друг другу. Пусть площадь самого маленького треугольника S1 и его основания a1, высота h1 и т.д., тогда

3S1=S3, a из подобия a1/a3=h1/h3

2S1=S2, a из подобия a1/a2=h1/h2

3a1h1/2=a3h3/2

3a1*a1h3/a3=a3h3

3a1²=a3²

a1=a3/√3

Аналогично

2a1h1/2=a2h2/2

2a1*a1*h2/a2=a2h2

2a1²=a2²

a2=√2a1=√2a3/√3

Итого

a1=a3/√3

а2==√2a3/√3

a3=a3 - странно :)

Именно в таком же соотношении будет делиться боковая сторона, если мы будем считать от вершины.

√3/3: √6/3 : 1 - избавился от иррациональности в знаменателе.

Внимание!!!! Смотри картинку с возможными разночтениями

Объяснение:

Приложения:

aarr04594: Десь помилка.

p15: 0.5773502691896257:0.8164965809277259:1 - похоже на правду. Очень похоже. Просто у нас разные ответы - смотрите мой рисунок

p15: Если умножить мой ответ на корень из 3, то получим то, что у вас слева на рисунке. Так что совпадает

aarr04594: Я эту задачу хорошо знаю. Имеется ввиду, от начала вершины , чтобы была запись в ответе в порядке х:у:z, а не наоборот, если смотреть на ваш рисунок.

p15: У меня ВСЕ отрезки от вершины. Я не учитель и не знаю эту задачу, но условие - рахуючи від вершини делить отрезки. :). Я так понимаю условие.

p15: Я честно написал что возможны разночтения условия

p15: Кроме того мне мой ответ удобно обрабатывать, как данные. Сначала надо взять 58%!!!!!, потом 82% от целой боковой стороны. И понятно почему так

aarr04594: Наверное, надо вникнуть в ваше решение , чтобы вести дискуссию. Ответ в учебнике: 1:(√2-1):(√3-√2).

p15: 1:(√2-1):(√3-√2). - легко получить из моего - мой же, как выяснили 1:√2:√3. (умножив на √3) Теперь просто - первый остается 1, от второго нужно отнять первый отрезок, в от третьего второй, вот и получаем 1:(√2-1):(√3-√2). Правда легко?

aarr04594: А, так мы с вами эту задачу 22-25 июня уже и обсуждали. И сошлись на том, что пусть будет два решения. Хотя позже автор вопроса в коментах подтвердил, что отношение отрезков такое, как "поняла" его я (и так знала). Но кто-то поставил тогда нарушение, модератор не разобрался и удалил. Удалил и удалил. Главное , что решение автор вопроса успел переписать.

Автор ответа: aarr04594

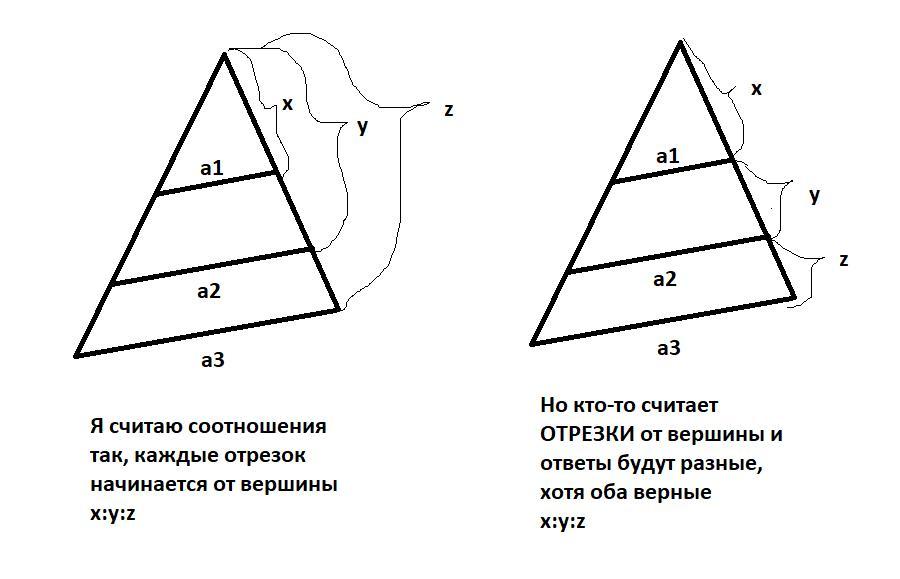
Відповідь: фото.

Пояснення:

розв'язання завдання додаю

Приложения: