СРОЧНО!!! 43 бала. Плоский кут при вершині правильної чотирикутної піраміди дорівнює α. Знайди відношення бічної поверхні піраміди до поверхні описаної навколо піраміди кулі.
Розв’яжи завдання з обґрунтуванням і поясненням.
Ответы
Ответ:
Sбок/Sсф = sin2α/π
Объяснение:
Плоский угол при вершине правильной четырехугольной пирамиды равен α. Найди отношение боковой поверхности пирамиды к поверхности описанной вокруг пирамиды сферы.
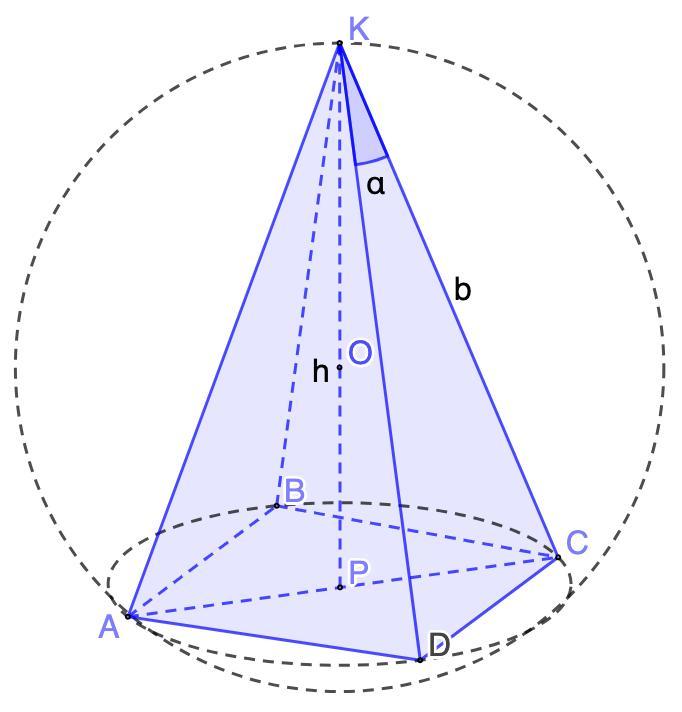
Дано: KABCD - правильная пирамида;
∠DKC = α;
Сфера(О) - описана около KABCD.
Найти: Sбок/Sсф
Решение:
- В основании правильной четырехугольной пирамиды лежит квадрат, а боковые грани - равные равнобедренные треугольники.
⇒ площадь боковой поверхности пирамиды равна сумме площадей четырех равных равнобедренных треугольников.
- Площадь треугольника равна половине произведения двух сторон на синус угла между ними.
Обозначим боковое ребро - b.
⇒ Sбок = 4 · 1/2 · b² sin α = 2b²sin α
Найдем площадь поверхности сферы по формуле:
Sсф = 4πR²
Радиус сферы, описанной около правильной пирамиды, равен:
R = b²/2h,
где b - боковое ребро, h - высота пирамиды.
Надо найти h.
Найдем сначала сторону основания по теореме косинусов.
- Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Рассмотрим ΔDKC - равнобедренный.
DC² = KD² + KC² - 2 · KD · KC · cos α
DC² = b² + b² - 2b²cos α = 2b²(1 - cos α)
Рассмотрим ΔАСD - прямоугольный.
- Теорема Пифагора:
- Квадрат гипотенузы равен сумме квадратов катетов.
АС² = DC² + AD² = 2b²(1 - cos α) + 2b²(1 - cos α) = 4b²(1 - cos α)
AC = 2b√(1-cos α) ⇒ AP = b√(1-cos α)
Рассмотрим ΔАКР - прямоугольный.
По теореме Пифагора:
АК² = АР² + КР²
КР² = b² - b²(1-cos α) = b²(1 - 1 + cos α) = b²cos α
⇒ KP = b√cos α
Высоту нашли. Можем найти радиус:
Площадь поверхности сферы:
Sсф = 4πb²/4cos α = πb²/cos α
Sбок/Sсф =
#SPJ1