Решите пожалуйста!!!
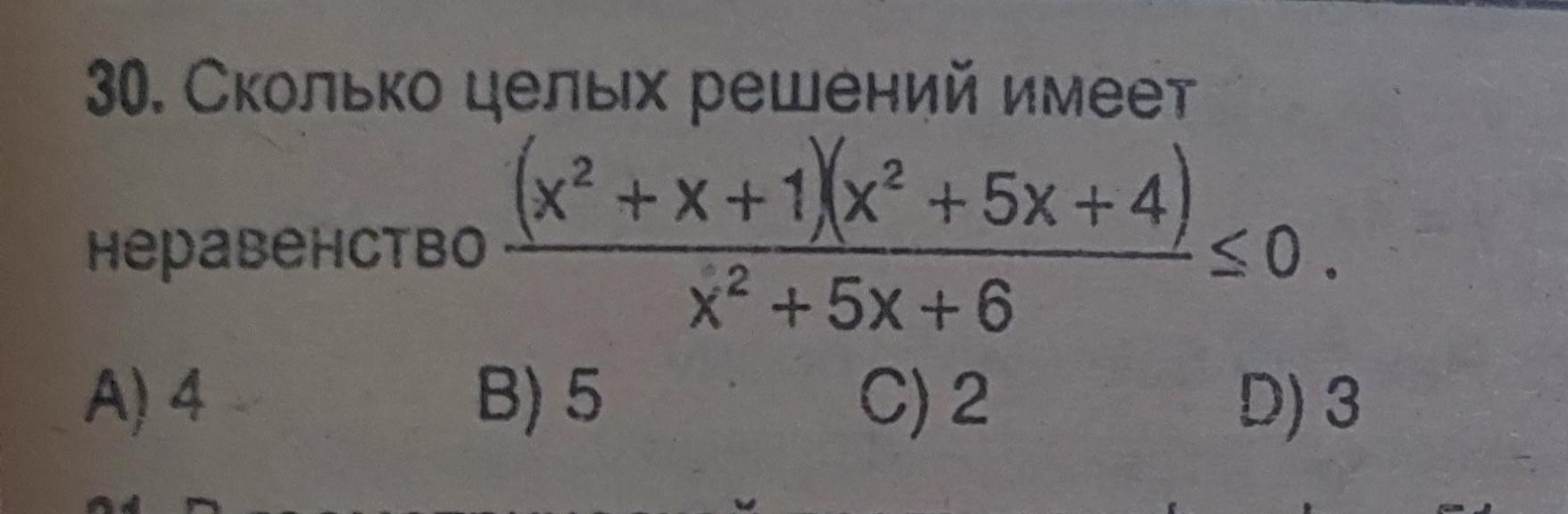
Ответы
Разложим на множители x² + x + 1 :
Дискриминант < 0 , старший коэффициент равен 1 > 0 , значит
x² + x + 1 > 0 при любых действительных значениях x .
Разделим на это выражение обе части неравенства , знак неравенства при этом не поменяется . Получим :
Два целых решения : - 4 и - 1
Відповідь: С ) 2 .
Пояснення:
( x² + x + 1 )( x² + 5x + 4 )/( x² + 5x + 6 ) ≤ 0 ;
x² + x + 1 > 0 для будь - яких хЄ R ; далі за теоремою Вієта маємо :
x² + 5x + 4 = ( х + 4 )( х + 1 ) ; x² + 5x + 6 = ( х + 3 )( х + 2 ) .
Дана нерівність рівносильна такій нерівності :
( х + 4 )( х + 1 )/[ ( х + 3 )( х + 2 ) ] ≤ 0 ; рішимо методом інтервалів :
+ - 4 -- - 3 + - 2 -- - 1 +
--------------------*-----------₀-------------₀-------------*---------------------->
/////////// ///////////// X
f(- 5 ) > 0 ; f(- 3,5 ) < 0 ; f(- 2,5 ) > 0 ; f(- 1,5 ) < 0 ; f( 0 ) > 0 .
Всі розв'язки нерівності : хЄ [- 4 ; - 3 ) U (- 2 ; - 1 ] .
Цілі розв'язки нерівності : х = - 4 ; - 1 .
В - дь : є 2 - а цілі розв'язки .