Question

Знайти найбільше та найменше значення функції: z=x^2+2xy-y^2-4x на області D: x=3, y=0, y=x+1.

Answer 1

Ответ:

Наибольшее и наименьшее значение функции: z наиб. = 6; z наим. = -4.

Пошаговое объяснение:

• Найти наибольшее и наименьшее значение функции: z = x²+2xy-y²-4x в области D: x=3, y=0, y=x+1.

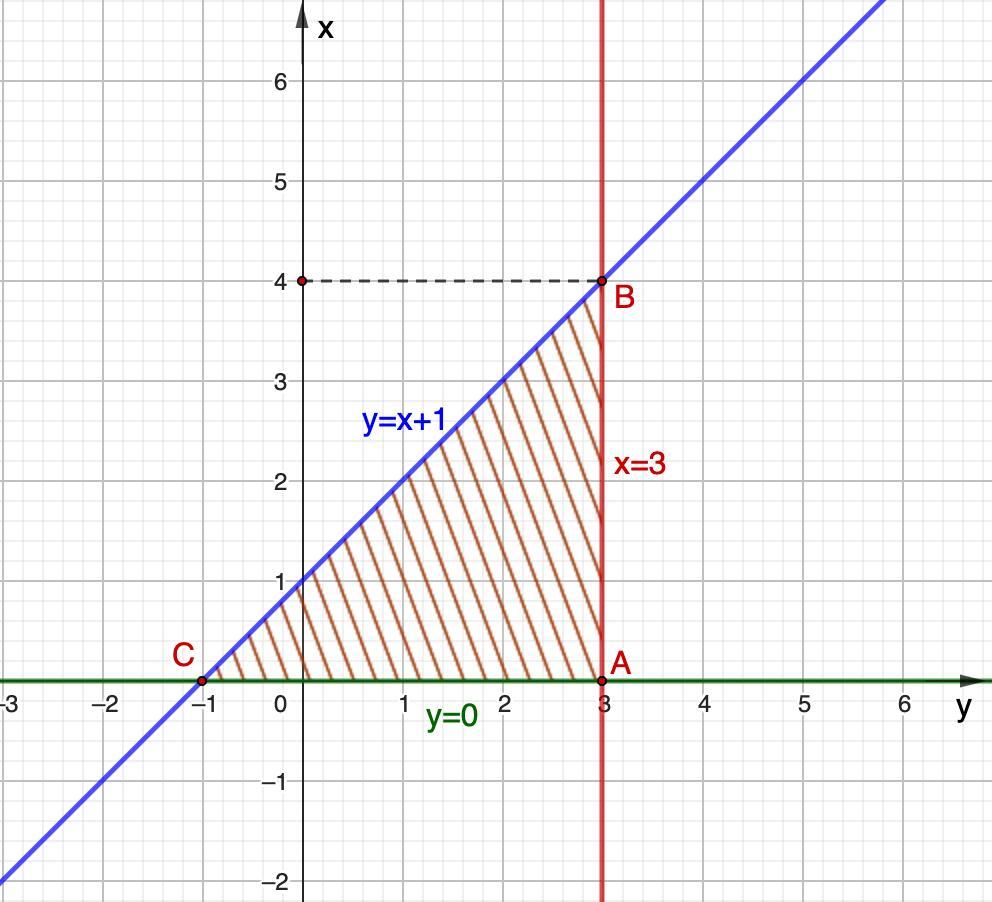
Строим область D.

Три пересекающихся прямых: x=3, y=0, y=x+1.

Получили треугольник АВС с вершинами А(3; 0), В(3, 4), С(-1; 0)

Находим стационарные точки области D из условия:

$\displaystyle \left \{ {{z_x'=0} \atop {z'_y=0}} \right.$

z = x² + 2xy - y² - 4x

$\displaystyle z_x'=2x+2y-4\\\\z_y'=2x-2y$

Найдем точки, в которых обе частные производные равны нулю (стационарные точки):

Решим систему:

$\displaystyle \left \{ {{2x+2y=4} \atop {2x-2y=0}} \right.$

Решим методом сложения:

4х = 4   ⇒   х = 1; у = 1

Получили точку М₀(1; 1) ∈ D.

$\displaystyle z(M_0)=1^2-2\cdot1\cdot1-1^2-4\cdot1=\boxed {\bf -2}$

Найдем стационарные точки на границах области D.

1. AC:   y = 0;   -1 ≤ x ≤ 3

z = x² -4x

Найдем производную и приравняем к нулю:

z'(x) = 2x - 4   ⇒   x = 2

$\displaystyle z(2)=2^2-4\cdot2=\boxed {\bf -4}$

Найдем значение функции на концах отрезка:

Точка А:   $\displaystyle z(3)=3^2-4\cdot3=\boxed {\bf -3}$

Точка С:   $\displaystyle z(-1)=(-1)^2-4\cdot(-1)=\boxed {\bf 5}$

2. AВ:  х = 3;   0 ≤ у ≤ 4

z = 3² + 6у - у² - 12 = -у² + 6у - 3

Найдем производную и приравняем к нулю:

z'(у) = -2у + 6   ⇒   у = 3

$\displaystyle z(3)=-3^2+6\cdot3-3=\boxed {\bf 6}$

Найдем значение функции на концах отрезка:

Точка А:   $\displaystyle z(0)=\boxed {\bf -3}$

Точка В:   $\displaystyle z(4)=-(4)^2+6\cdot4-3=\boxed {\bf 5}$

3. ВС:  у = х + 1;   -1 ≤ х ≤ 3

z = х² + 2х · (х + 1) - (х + 1)² - 4х = х² + 2х² +2х - х² - 2х - 1 - 4х =  2х² - 4х - 1

Найдем производную и приравняем к нулю:

z'(х) =4х - 4   ⇒   х = 1

$\displaystyle z(1)=2\cdot1^2-4\cdot1-1=\boxed {\bf -3}$

Найдем значение функции на концах отрезка:

Точка C:   $\displaystyle z(-1)=2\cdot(-1)^2-4\cdot(-1)-1=\boxed {\bf 5}$

Точка В:   $\displaystyle z(3)=2\cdot3^2-4\cdot3-1=\boxed {\bf 5}$

Теперь из полученных значений осталось выбрать наибольшее и наименьшее значения.

z наиб. = 6; z наим. = -4

#SPJ1