Предмет: Математика,
автор: Orazbibi94
(sinx)^2+(sin2x)^2=(sin3x)^2
Ответы
Автор ответа:
0
Ответ:
πk, k c Z
± π/2 + πk, k c Z
± π/6 + πk, k c Z
Пошаговое объяснение:
на фото
Приложения:
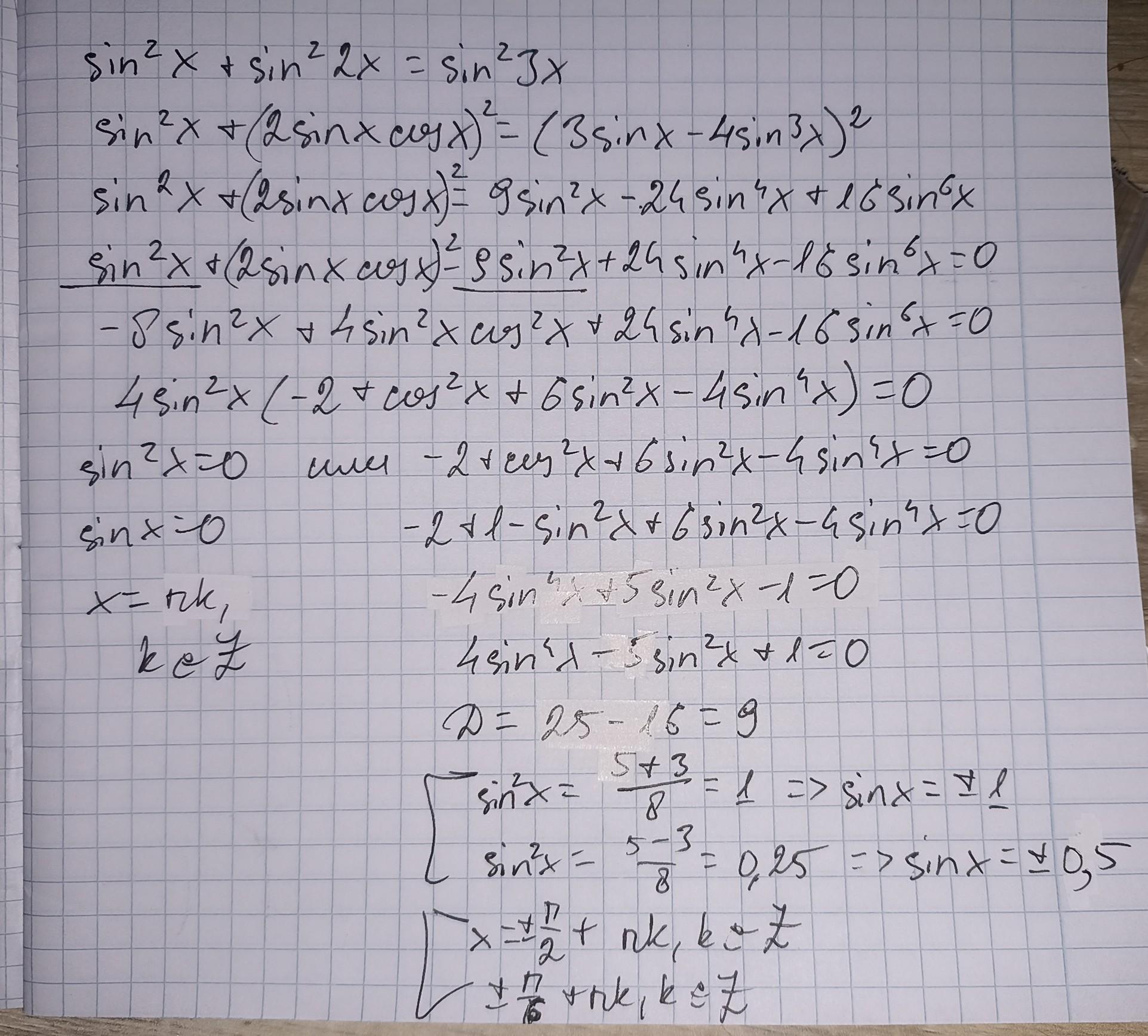
Автор ответа:
0
Ответ: x∈{ πk; π/2+πk; ±π/6+πk} k∈Z
Пошаговое объяснение:
(sinx)²+(sin2x)²=(sin3x)²
sin²x +(2sinx·cosx)²=(sin2x·cosx+cos2x·sinx)²
sin²x(1+4cos²x) =(2sinx·cosx·cosx +(cos²x-sin²x)·sinx)²
sin²x(1+4cos²x) = sin²x·(2·cos²x +cos²x-sin²x)²
sin²x=0 ; 1+4cos²x=(3cos²x-sin²x)²
x1=πk, k∈Z
1+4cos²x=(3cos²x-(1-cos²x))²
1+4cos²x=(4cos²x-1)²
1+4cos²x=16(cosx)^4+1-8cos²x
16(cosx)^4-12cos²x=0
cos²x=0 ; 4cos²x-3=0
x2=π/2+πk, k∈Z
cos²x=3/4 => cosx=±√3/2
x3=±π/6+πk ,k∈Z
x∈{ πk; π/2+πk; ±π/6+πk} k∈Z
Похожие вопросы
Предмет: Українська мова,
автор: cone02wz
Предмет: Українська література,
автор: vladdichuk176
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: gazorpasorpfield
Предмет: Английский язык,
автор: Georgyupi7